এখানে আমরা অমূলদ সংখ্যা নিয়ে আরেকটু বেশি কিছু জানার চেষ্টা করব।
আমরা তো Numbers থেকে দেখেছি যে অমূলদ সংখ্যা কি:
যে সকল দশমিক ভগ্নাংশে দশমিক বিন্দুর পরে অসীম সংখ্যক non-repeating ভ্যালু আসতেই থাকে তাদেরকে অমূলদ সংখ্যা বা Irrational Number বলে। এদের দশমিকের পরের ভ্যালু কখনো শেষও হয়না আবার বারবার repeat ও করেনা! অর্থাৎ এরা অসীম অনাবৃত্ত দশমিক ভগ্নাংশ।
যেমন, π এর মান ৩.১৪১৫৯২৬৫৩….. এভাবে একের পর এক অংক আসতেই থাকে কিন্তু পরের অংকটি কি আসবে তা আগে থেকে বোঝা যায় না বা কোনো প্যাটার্ন ফলো করেনা অর্থাৎ এক্ষেত্রে একটা নির্দিষ্ট ঘর পর্যন্ত পরপর একই অংকের পুনরাবৃত্তি ঘটেনা। সবচেয়ে জনপ্রিয় অমূলদ সংখ্যা হল \sqrt ২ (একে পীথাগোরাসের ধ্রুবক বলা হয়) যার মান ১.৪১৪২১৩…… এখানেও এভাবে অসীম পর্যন্ত non-repeating value আসতে থাকে তাই এরা সবাই অমূলদ সংখ্যা।
অন্য কথায় বলা যায়, যে সকল সংখ্যাকে দুইটি পূর্ণ সংখ্যার অনুপাত আকারে প্রকাশ করা যায় না তাদেরকে অমূলদ সংখ্যা বলে। যেমন, ১.৩৩৩৩৩৩৩৩… … এটা মূলদ সংখ্যা কেননা একে \frac ৪ ৩ (৪ ও ৩ এর অনুপাত) আকারে লেখা যায়। কিন্তু π বা ৩.১৪১৫৯২৬৫৩….. , \sqrt ২ বা ১.৪১৪২১৩….. এদেরকে এরকম লব : হর বা \frac {লব} {হর} আকারে লেখা যায় না, গেলে তো আর সে অমূলদ থাকত না মূলদ হয়ে যেত।
** আচ্ছা π জিনিসটা কি? এর নাম হল pi বা পাই। বৃত্ত তো আমরা সবাই চিনি, এই বৃত্তের পরিধি ও ব্যাসের অনুপাত করলে যা পাই মানে যা পাওয়া যায় তাই হল আমাদের পাই মানে π। যেমন, আমরা সবাই জানি যে বৃত্তের পরিধি হল 2πr আর ব্যাস হল 2r, তাহলে \frac {পরিধি} {ব্যাস} = \frac {2πr} {2r} = π আর এর মান ৩.১৪১৫৯২৬৫৩….. এভাবে অসীম পর্যন্ত একের পর এক অংক আসতেই।
তাহলে সহজে কিভাবে অমূলদ সংখ্যা চিনব: আসলে যেকোন দুইটা পূর্ণ সংখ্যার মধ্যে গাদি গাদি ভগ্নাংশ আছে যেমন,
২ ও ৩ এর মাঝে আছে ২.৩, ২.৪, ২.৫, ২.৬, ২.৭ ইত্যাদি। আবার
২.৩ ও ২.৪ এর মাঝে আছে ২.৩১, ২.৩২, ২.৩৩, ২.৩৪ ২.৩৫ ইত্যাদি। আবার
২.৩১ ও ২.৩২ এর মাঝে আছে ২.৩১০১, ২.৩১০২, ২.৩১০৩, ২.৩১০০০২ ইত্যাদি
এভাবে যেকোন দুইটা ভগ্নাংশের মধ্যেও গাদি গাদি ভগ্নাংশ আছে। এতক্ষন যাদের দেখলাম তারা তো সবাই মূলদ সংখ্যা। ঠিক একই ভাবে এদের মধ্যে আছে অসীম সংখ্যক অমূলদ সংখ্যা। এখন নিচের উদাহরন দুইটা দেখি:
(এসব কিছুটা জটিল ব্যাপার তাই কিছুটা বেশি মনোযোগ দিয়ে দেখতে হয়)
\frac {২২} {৭}
= ৩.১৪২৮৫৭১৪২৮৫৭… …
= ৩.\dot ১৪২৮৫\dot ৭
এবং
\frac {২৩} {৭}
= ৩.২৮৫৭১৪২৮২৮৫৭১৪… …
= ৩.\dot ২৮৫৭১\dot ৪
এদের মধ্যেও অসীম সংখ্যক মূলদ ও অমূলদ সংখ্যা আছে। যেমন, ৩.১৫০৯০০৮০৬৭০৪৫… … , ৩.১৬০০০৮০৭৮৪০৯৯৫… … , ৩.১৭৬৮৫৬০৬৭০৪৫… … ইত্যাদি অমূলদ সংখ্যা। আবার
৩.১৫০৯০০৮০৬৭০৪৫… … ও ৩.১৬০০০৮০৭৮৪০৯৯৫… … এর মধ্যেও অসীম সংখ্যক মূলদ ও অসীম সংখ্যক অমূলদ সংখ্যা আছে। যেমন,
৩.১৫০৯১, ৩.১৫১০৮, ৩.১৫০৯০৯ ইত্যাদি হল মূলদ সংখ্যা আর
৩.১৫০৯২৩২৩৪৩৫০৪৫… … , ৩.১৫১০০৮০৬৫৪৬৪৭৫৭৫… … , ৩.১৫৯৮৬৬৫০৬৭০৪৫… …, ৩.১৫৯৯৮৭০০৭৮৪০৯৯৫… … ইত্যাদি হল অমূলদ সংখ্যা।
আচ্ছা এবার একটু সহজ ভাবে চিন্তা করি, আমরা তো সবাই জানি \sqrt ২, \sqrt ৩, \sqrt ৫ এরা অমূলদ সংখ্যা কারন এদেরকে দশমিক ভগ্নাংশে রুপান্তরিত করলে দেখা যায় \sqrt ২ = ১.৪১৪২১৩… … এখানে দশমিকের পর অসীম সংখ্যক অজানা ভ্যালু আসতে থাকে। একই ভাবে \sqrt ৩ = ১.৭৩২০৫০৮০৭৫৬৮৮৭৭২৯… … , \sqrt ৫ = ২.২৩৬০৬৭৯৭৭৪৯৯৭৮৯৬… … তাই এরা সবাই অমূলদ সংখ্যা। আচ্ছা আমার \sqrt ৪ কি দোষ করল? \sqrt ৪ = ২ আর ২ ভগ্নাংশ তো নয়ই বরং পূর্ণ সংখ্যা সুতরাং তার অমূলদ হওয়ার প্রশ্নই উঠেনা বরং সে তরতাজা মূলদ সংখ্যা। এভাবে আমরা খেয়াল করলে দেখতে পাই যে, সকল পূর্ণবর্গ সংখ্যার বর্গমূল হল মূলদ সংখ্যা (যে সকল সংখ্যাকে বর্গমূল করলে একটি পূর্ণ সংখ্যা পাওয়া যায় তাদেরকে পূর্ণবর্গ সংখ্যা বলা হয়)। যেমন, \sqrt ৯ = ৩, \sqrt {১.৪৪} = ১.২, \sqrt {১২.২৫} = ৩.৫ আবার পূর্ণবর্গ নয় এরকম সকল সংখ্যার বর্গমূলই হল অমূলদ সংখ্যা। যেমন, \sqrt ৭, \sqrt ১১, \sqrt ১২ ইত্যাদি। এর বাইরে ও ভিতরে অসংখ্য মূলদ ও অমূলদ সংখ্যা আছে (উপরে তার কিঞ্চিত নমুনা দেখেছি)।
ঠিক একই ভাবে আমরা দেখতে পাই যে, সকল পূর্ণঘন সংখ্যার ঘনমূল হল মূলদ সংখ্যা (যে সকল সংখ্যাকে ঘনমূল করলে একটি পূর্ণ সংখ্যা পাওয়া যায় তাদেরকে পূর্ণঘন সংখ্যা বলা হয়)। যেমন, \sqrt[৩] ৮ = ২, \sqrt[৩] {২৭} = ৩। আবার পূর্ণঘন নয় এরকম সকল সংখ্যার ঘনমূলই হল অমূলদ সংখ্যা। যেমন, \sqrt[৩] {২} = ১.২৫৯৯২১০৪৯৮৯৪৮৭৩১… , \sqrt[৩] {১১} = ২.২২৩৯৮০০৯০৫৬৯৩১৫৫২১… , \sqrt[৩] {২২} = ২.৮০২০৩৯৩৩০৬৫৫৩৮৭১… ইত্যাদি।
এখানে, আমরা যে বর্গমূল, ঘনমূল করতেছি এগুলো কিন্তু শুধুমাত্র ধনাত্নক সংখ্যার ক্ষেত্রে প্রযোজ্য। কারন ঋনাত্নক সংখ্যার বর্গমূল, ঘনমূল করলে তখন বাস্তব সংখ্যার সাথে আরো কিছু কাল্পনিক অংশ যুক্ত হয়ে জটিল সংখ্যা হয়ে যায়। এ নিয়ে অন্য পোষ্টে আলোচনা হবে।
মনে একটা প্রশ্ন আসে, {\sqrt ২}^{\sqrt ৩} কি মূলদ নাকি অমূলদ সংখ্যা? {\sqrt ২}^{\sqrt ৩} এর মান হল 1.822634654966242214393768215… … তো এখানেও একই ব্যাপার, অসীম পর্যন্ত non-repeating ভ্যালু আসতেছে সো {\sqrt ২}^{\sqrt ৩} ও অমূলদ সংখ্যা।
একই ভাবে {\sqrt ২}^{\sqrt ২} = 1.6325269194381528447734953810247196020791088570531141172477806843… ও অমূলদ সংখ্যা।
মনে আরেকটা প্রশ্ন আসে, কোনো সংখ্যার দশমিকের পরের ১০০ বা ১০০০ টা non-repeating ভ্যালুর পর যদি অসীম সংখ্যক repeating ভ্যালু আসতে থাকে যেমন, ৩.১২৩২১৪৩৫৬৭৮৯৮৭৭০৯৮৮৭৯৯৮৮৮৮৯৮৯৮৯৮৯২৩৭৮১০০৯৭৯৮৯৮৯২৩৭৮১০০৯৭… … বা
৩.১২৩২১৪৩৫৬৭৮৯৮৭৭০৯৮৮৭৯৯৮৮৮৮\dot ৯৮৯৮৯৮৯২৩৭৮১০০৯\dot ৭। তাহলে কি সে মূলদ হবে নাকি অমূলদ হবে? আমরা মূলদ সংখ্যার সংগা থেকে জানি non-repeating ভ্যালু থাকলেই সে মূলদ সংখ্যা কেননা তখন তাকে \frac {লব} {হর} আকারে লেখা যায় অর্থাৎ ইনিও মূলদ সংখ্যা।
কিন্তু যদি, কোন ভগ্নাংশ অসীম অনাবৃত্ত হয় এবং তার non-repeating ডিজিট গুলো একটা প্যাটার্ন ফলো করে আগাতে থাকে তাহলে কি হবে? যেমন, 1.01001000100001000001000000100000001… … ,
2.0200220002220000222200… … ,
4.12301230012300012300001230000012300… …
এরকম ভগ্নাংশ কি মূলদ হবে নাকি অমূলদ হবে? আমরা জানি যাদেরকে \frac {লব} {হর} আকারে লেখা যায় তারা মূলদ সংখ্যা অথবা যারা সসীম দশমিক ভগ্নাংশ অথবা যারা অসীম আবৃত্ত দশমিক ভগ্নাংশ তারা সবাই মূলদ সংখ্যা। আর যারা অসীম অনাবৃত্ত দশমিক ভগ্নাংশ তারা সবাই অমূলদ সংখ্যা। উপরের ভগ্নাংশ গুলো সবাই অসীম অনাবৃত্ত অর্থাৎ non-repeating ডিজিট গুলো একটা প্যাটার্ন ফলো করতেছে ঠিকই কিন্তু একই সংখ্যক ডিজিটের পুনরাবৃত্তি ঘটতেছেনা। তাই এরা সবাই অমূলদ সংখ্যা।
এখন দেখি অমূলদ সংখ্যা কত রকমের হতে পারে:
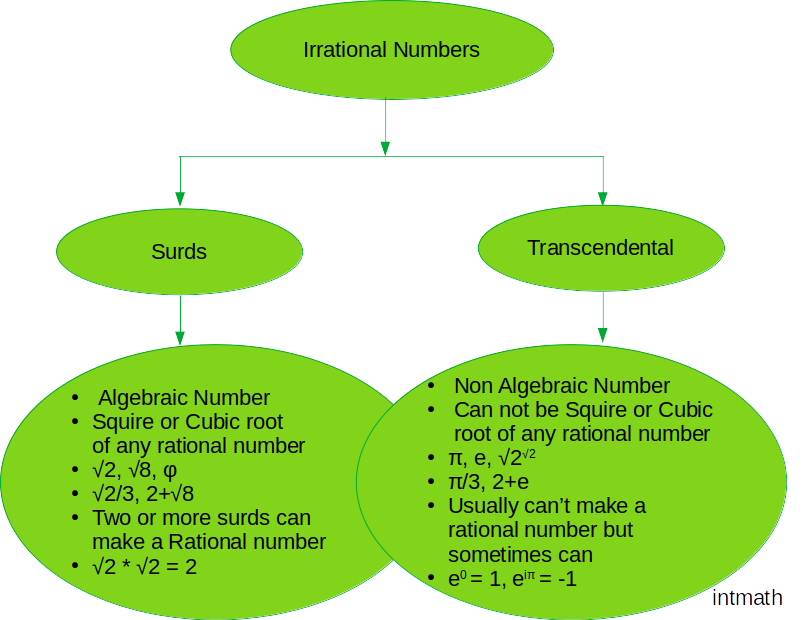
তাহলে অমূলদ সংখ্যা মূলত দুই প্রকার:
1. Surds
2. Transcendental
1. Surds: সাধারন ভাবে Surd হল radical symbol বা root symbol তা সে squire root হোক আর cubic root হোক। যেমন, \sqrt[n] X। অর্থাৎ integer বা কোনো বহুপদীর বর্গমূল বা ঘনমূল করে যে সকল মূল বা সমাধান পাওয়া যায় তারা হল Surds। যেমন, \sqrt ২, \sqrt ৩ ইত্যাদি। এরা algebraic number।
এখন দেখব Transcendental Number কিন্তু ইনাদেরকে চিনতে হলে তার আগে আমাদের algebraic number কি তা জানতে হবে।
Algebraic Number: খুব অল্প এবং খুব সহজ কথায়, যে সকল number কে algebra বা বীজগানিতীয় সমীকরনের মাধ্যমে সমাধান করা যায় বা সত্য হিসেবে প্রমান করা যায় তারা হল Algebraic Number। ভালমতো বুঝলাম নাহ। আচ্ছা নিচের উদাহরন গুলো মনোযোগ দিয়ে দেখলে ভালমতো বোঝা যাবে।
যেমন,
2x3 − 5x + 6 = 0 এটা একটা বীজগানিতিক সমীকরন, এখানে x এর ভ্যালু নির্নয় করতে হবে। আমরা দেখি x = -2 নিলে কি হয়:
2*(-2)3 − 5*(-2) + 6 = 0
বা 2*(-8) + 10 + 6 = 0
বা – 16 + 10 + 6 = 0
বা -16 + 16 = 0
বা, 0 = 0 হয়,
অর্থাৎ x = -2 নিলে সমীকরনটি সত্য হয়, তাহলে -2 হল algebraic number.
কিন্তু একটা কথা আছে, বীজগানিতিক সমীকরনটির কিছু শর্ত পুরন করতে হয়। যেমন,
১। সমীকরনের যেকোনো একপাশে একটা বহুপদী থাকতে হবে।
২। বহুপদীটি কে non-zero বা অশুন্য হতে হবে।
৩। বহুপদীর সবগুলো পদের সহগ অশুন্য এবং মূলদ সংখ্যা হতে হবে।
৪। এবং x হবে সমীকরনটির মূল।
যেমন, উপরের সমীকরনটির বহুপদীটি হল
১। 2x3 − 5x + 6 যার ৩ টি পদ আছে।
২। সে অশুন্য।
৩। তার সবগুলো পদের সহগ (২, -৫, ৬) অশুন্য এবং rational number বা মূলদ সংখ্যা।
আচ্ছা বহুপদী কি জিনিস তা আস্তে করে দেখে নিই:
বহুপদী হল যার বহু বা একের অধিক পদ আছে, এরা রাশিও হতে পারে আবার সমীকরনও হতে পারে। যেমন, 3x – 4, 2x3 − 5x + 6 ইত্যাদি হল বহুপদী রাশি আর 3x – 4 = 0, 2x3 − 5x + 6 = 0 ইত্যাদি হল বহুপদী সমীকরন। তো কোনো বহুপদীর ২টা পদ থাকলে তাকে দ্বিপদী রাশি বা সমীকরন বলে, ৩টা পদ থাকলে তাকে ত্রিপদী রাশি বা সমীকরন বলে।
তাহলে 2x2 + 2x* 3y + 5 = 2 এটা কয়পদী সমীকরন? ব্যাপারটা নিচে দেখি:
2x2 + 2x* 3 + 5 = 2
বা, 2x2 + 6x + 5 – 2 = 0
বা, 2x2 + 6x + 3 = 0
আপাত ভাবে দেখে ৪ বা ৫ পদী মনে হলেও আসলে সে ত্রিপদী সমীকরন!
এখন আমরা আবার algebraic number দেখি:
* 2 – 2 = 0 বা x – 2 = 0 [যেখানে x=2]
* 3(\frac {4} {3}) – 4 = 0 বা 3x – 4 = 0 [যেখানে x = \frac {4} {3}]
* (\sqrt {2})2 - 2 = 0 বা x2 - 2 = 0 [যেখানে x = \sqrt {2}]
* (\sqrt {-1})2 + 1 = 0 বা x2 + 1 = 0 [যেখানে x = \sqrt {-1}]
তাহলে আমরা দেখতে পাচ্ছি, 2, \frac {4} {3}, \sqrt {2}, \sqrt {-1} বা i হল algebraic number। এভাবে আসলে সকল integer, fraction, rational number ই algebraic number, কিছু irrational number ও algebraic যেমন, surds ( \sqrt {2}, \sqrt {3}) আর যে সকল নাম্বার non-algebraic তারা হল Transcendental।
এখন দেখি, বিশিষ্ট mathematician মার্ক বার (Mark Barr) এর golden ratio বা 𝛗 (phi বা ফাই) কি algebraic নাকি non-algebraic অর্থাৎ Surd নাকি Transcendental:
𝛗 এর মান হল: 1.61803398875... ... অর্থাৎ সে অমূলদ সংখ্যা।
এখন,
x2 − x − 1 = 0 এটা একটা non-zero বহুপদী সমীকরন যার সবগুলো পদের সহগ (১, -১, -১) অশুন্য এবং মূলদ সংখ্যা। একে সমাধান করে দেখি কি পাওয়া যায়:
x2 − x − 1 = 0
বা, x = \frac {-(-1)±\sqrt {(-1)^2- 4\cdot1\cdot(-1)}} {2\cdot1}
[আমরা জানি দ্বিঘাত সমীকরনের মূল, x = \frac {-b±\sqrt {b^2- 4\cdot a\cdot c}} {2\cdot a}]
বা, x = \frac {1 ± \sqrt {1 + 4}} {2}
বা, x = \frac {1 ± \sqrt {5}} {2}
বা, x = \frac {1 + \sqrt {5}} {2} অথবা x = \frac {1 - \sqrt {5}} {2}
বা, x = 1.61803398875... ... অথবা x = .61803398875... ...
এখন দেখি, x = 1.61803398875... ... এই মান টা কেমন জানি চেনা চেনা লাগছে...
একটু আগেই দেখেছি 𝛗 এর মান হল: 1.61803398875... ... (ইয়েস মিলগেয়া!!)
তাহলে 𝛗 হল আমাদের algebraic number!! অর্থাৎ 𝛗 হল একটা Surd 💙
2. Transcendental: Transcendental কি তা আমরা অলরেডি জেনে গিয়েছি!! একটু আগেই দেখেছি যে, যে সকল নাম্বার non-algebraic তারা হল Transcendental। অর্থাৎ যাদেরকে কোনো পূর্ণসংখ্যার বর্গমূল, ঘনমূল এভাবে করে পাওয়া যায় না অর্থাৎ যে সকল number কে algebra বা বীজগানিতীয় সমীকরনের মাধ্যমে সমাধান করা যায় না বা সত্য হিসেবে প্রমান করা যায় না তারা হল Transcendental বা non-Algebraic Number। যেমন, π, e ( ইনি হলেন ইউলার ধ্রুবক) ইত্যাদি।
আমরা তো জানি সকল বাস্তব সংখ্যাকে সংখ্যারেখার উপর চিহ্নিত করা যায় বা জায়গা দেওয়া যায়। ধনাত্নক, ঋণাত্নক, পূর্ণ সংখ্যা, দশমিক সংখ্যা বা ভগ্নাংশদেরকে যে সংখ্যারেখার উপর চিহ্নিত করা যায় অর্থাৎ সংখ্যারেখার উপর তাদের প্রত্যেকের জন্য একটা নির্দিষ্ট জায়গা আছে তা Numbers এ দেখেছি। কিন্তু কতগুলো প্রশ্ন আছে যে, অমূলদ সংখ্যাকে কি সংখ্যারেখার উপর চিহ্নিত করা যায়? তাদের তো দশমিকের পরে অসীম সংখ্যক অংক আসতে থাকে যাদেরকে নির্দিষ্টই করা যায় না তাহলে কেমন করে সংখ্যারেখার উপর তার জায়গাটা নির্দিষ্ট করব? অমূলদ সংখ্যাও তো বাস্তব সংখ্যা তাই প্রথম প্রশ্নের উত্তর হল, হ্যাঁ, অমূলদ সংখ্যাদেরকেও সংখ্যারেখার উপর চিহ্নিত করা যায়। কিভাবে তার জায়গাটা নির্দিষ্ট করা যায় তা নিচের ছবিগুলো থেকে দেখি ও বুঝি:
\sqrt 2:
প্রথমে দেখি সংখ্যারেখার উপর ঠিক কোন জায়গাটায় \sqrt 2 আরামে বসে আছে। নিচের ছবিটি (খুপ খেয়াল কইরা) দেখি:
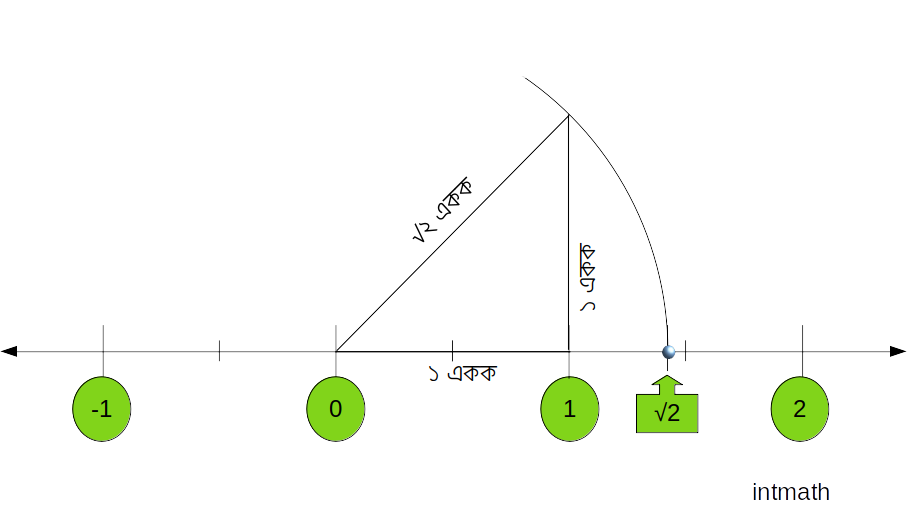
এখানে সমকোণী ত্রিভুজটির ভুমি ১ একক ও লম্ব ১ একক। গুরু পীথাগোরাসের উপপাদ্য অনুসারে আমরা জানি, কোনো সমকোণী ত্রিভুজের, অতিভুজ2 = লম্ব2 + ভুমি2 ।
তাহলে উপরের সমকোণী ত্রিভুজটির ক্ষেত্রে,
অতিভুজ2 = 12 + 12
বা, অতিভুজ2 = 2
বা, অতিভুজ = \sqrt 2
তাহলে উপরের সমকোণী ত্রিভুজটির অতিভুজ পেলাম \sqrt 2 একক। অর্থাৎ অতিভুজটির দৈর্ঘ্য পেলাম \sqrt 2। এখন তাহলে অতিভুজটির এক প্রান্ত শূণ্যের উপর ধরে (সংখ্যারেখার উপর যেখানটাই শুন্য অবস্থিত) অতিভুজটিকে সংখ্যারেখার উপর রাখলে তার অন্য প্রান্ত যে বিন্দুতে শেষ হয় শুন্য থেকে ঐ বিন্দু পর্যন্ত দূরত্বই হল আমাদের কাঙ্খিত \sqrt 2 একক দূরত্ব। তাহলে শুন্যকে কেন্দ্র করে ত্রিভুজটির অতিভুজটিকে ব্যাসার্ধ ধরে শুন্য থেকে ডানদিকে (কারন ধনাত্নক সংখ্যাগুলো শুন্য থেকে ডানদিকে অবস্থিত) সংখ্যারেখার উপর একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি সংখ্যারেখার ঠিক যে বিন্দুর উপর দিয়ে যায় ঠিক ঐ বিন্দুটাই হল \sqrt 2 এর ঠিকানা।
\sqrt 5:
\sqrt 5 এর ঠিকনাও \sqrt 2 এর মত করে দেখানো যায়। নিচের ছবিটি মনোযোগ দিয়ে দেখি:
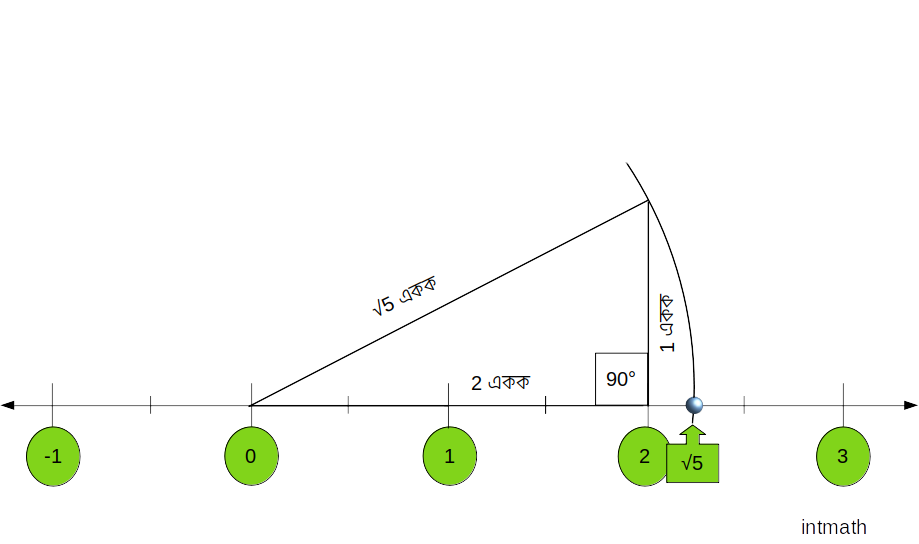
এখানে সমকোণী ত্রিভুজটির ভুমি ২ একক ও লম্ব ১ একক। তো আবারো গুরু পীথাগোরাসের উপপাদ্য অনুসারে আমরা জানি, কোনো সমকোণী ত্রিভুজের, অতিভুজ2 = লম্ব2 + ভুমি2 ।
তাহলে উপরের সমকোণী ত্রিভুজটির ক্ষেত্রে,
অতিভুজ2 = 22 + 12
বা, অতিভুজ2 = 4 + 1
বা, অতিভুজ2 = 5
বা, অতিভুজ = \sqrt 5
তাহলে উপরের সমকোণী ত্রিভুজটির অতিভুজ পেলাম \sqrt 5 একক। অর্থাৎ অতিভুজটির দৈর্ঘ্য পেলাম \sqrt 5। এখন তাহলে অতিভুজটির এক প্রান্ত শূণ্যের উপর ধরে (সংখ্যারেখার উপর যেখানটাই শুন্য অবস্থিত) অতিভুজটিকে সংখ্যারেখার উপর রাখলে তার অন্য প্রান্ত যে বিন্দুতে শেষ হয় শুন্য থেকে ঐ বিন্দু পর্যন্ত দূরত্বই হল আমাদের কাঙ্খিত \sqrt 5 একক দূরত্ব। তাহলে শুন্যকে কেন্দ্র করে ত্রিভুজটির অতিভুজটিকে ব্যাসার্ধ ধরে শুন্য থেকে ডানদিকে (কারন ধনাত্নক সংখ্যাগুলো শুন্য থেকে ডানদিকে অবস্থিত) সংখ্যারেখার উপর একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি সংখ্যারেখার ঠিক যে বিন্দুর উপর দিয়ে যায় ঠিক ঐ বিন্দুটাই হল \sqrt 5 এর ঠিকানা।
\sqrt 2, \sqrt 5 এগুলোর জায়গা তো সহজেই দেখানো যায়, পারলে \sqrt 3 কোথায় অবস্থিত দেখান তো।
ওকেই এখন তাইলে আমরা \sqrt 3 সংখ্যারেখার উপর ঠিক কোন জায়গাটায় বসে আছে সেটা খুঁজে বের করি:
\sqrt 3:
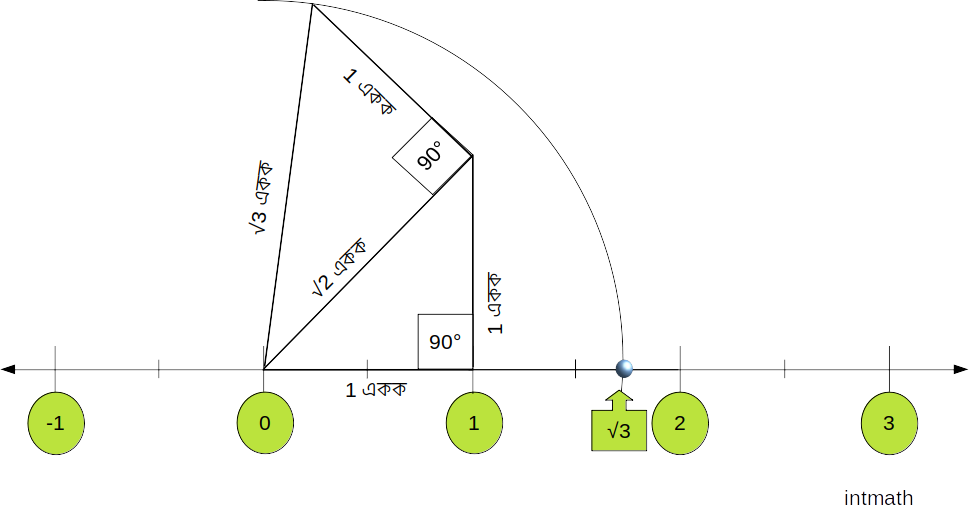
আমরা তো অলরেডি \sqrt 2 এর ঠিকানা খুঁজে পেয়েছি। তো \sqrt 2 এর ঠিকানা খোঁজার সময় ১ একক লম্ব ও ১ একক দৈর্ঘ্যের সমকোণী ত্রিভুজটির অতিভুজ পেয়েছিলাম \sqrt 2। এখন আমরা ঐ ত্রিভুজের শীর্ষ্য বিন্দুতে (উপরের চিত্রটি দেখি) \sqrt 2 একক দৈর্ঘ্যের অতিভুজের উপর ১ একক দৈর্ঘ্যের আরেকটি লম্ব আঁকি। তারপর শুন্যের বিন্দু (শুন্য অবস্থিত যে বিন্ধুতে) এবং নতুন অঙ্কিত লম্বের শীর্ষবিন্দু যোগ করি, তাহলে আমরা আরেকটি সমকোণী ত্রিভুজ পেলাম যার ভুমি হল \sqrt 2 একক এবং লম্ব হল ১একক। তাহলে আবারো গুরু পীথাগোরাসকে স্বরণ করি। তাঁর উপপাদ্য অনুসারে আমরা জানি, কোনো সমকোণী ত্রিভুজের, অতিভুজ2 = লম্ব2 + ভুমি2 ।
তাহলে উপরের নতুন অঙ্কিত সমকোণী ত্রিভুজটির ক্ষেত্রে,
অতিভুজ2 = (\sqrt 2)2 + 12
বা, অতিভুজ2 = 2 + 1
বা, অতিভুজ2 = 3
বা, অতিভুজ = \sqrt 3
তাহলে উপরের নতুন অঙ্কিত সমকোণী ত্রিভুজটির অতিভুজ পেলাম \sqrt 3 একক। অর্থাৎ অতিভুজটির দৈর্ঘ্য পেলাম \sqrt 3। এখন তাহলে অতিভুজটির এক প্রান্ত শূণ্যের উপর ধরে (সংখ্যারেখার উপর যেখানটাই শুন্য অবস্থিত) অতিভুজটিকে সংখ্যারেখার উপর রাখলে তার অন্য প্রান্ত যে বিন্দুতে শেষ হয় শুন্য থেকে ঐ বিন্দু পর্যন্ত দূরত্বই হল আমাদের কাঙ্খিত \sqrt 3 একক দূরত্ব। তাহলে শুন্যকে কেন্দ্র করে নতুন অঙ্কিত ত্রিভুজটির অতিভুজটিকে ব্যাসার্ধ ধরে শুন্য থেকে ডানদিকে (কারন ধনাত্নক সংখ্যাগুলো শুন্য থেকে ডানদিকে অবস্থিত) সংখ্যারেখার উপর একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি সংখ্যারেখার ঠিক যে বিন্দুর উপর দিয়ে যায় ঠিক ঐ বিন্দুটাই হল \sqrt 3 এর ঠিকানা।
\sqrt 9 বা 3:
এখন তাহলে আমরা \sqrt 9 সংখ্যারেখার উপর ঠিক কোন জায়গাটায় বসে আছে সেটা খুঁজে বের করি। কারন আমরা জানি \sqrt 9 = 3 তাহলে \sqrt 9 এর জায়গা যদি আমরা 3 যে বিন্দুতে অবস্থিত ঠিক সেই বিন্দুতেই নির্ণয় করতে পারি তাহলে বুঝবো যে উপরের \sqrt 2, \sqrt 3, \sqrt 5 অবস্থান ও ঠিক ঠিক ভাবে নির্ণয় করতে পেরেছি।
এখন তাহলে নিচের চিত্র ও বর্ণনা মনোযোগ সহকারে দেখি:
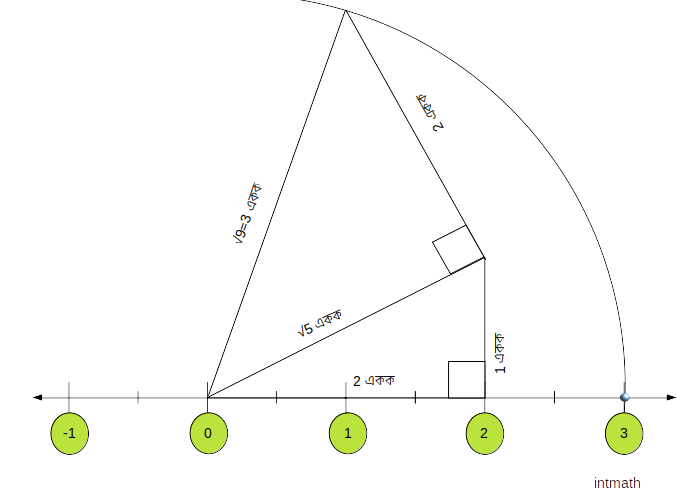
আমরা তো অলরেডি \sqrt 5 এর ঠিকানা খুঁজে পেয়েছি। তো \sqrt 5 এর ঠিকানা খোঁজার সময় ১ একক লম্ব ও ২ একক ভুমির সমকোণী ত্রিভুজটির অতিভুজ পেয়েছিলাম \sqrt 5। এখন আমরা ঐ ত্রিভুজের শীর্ষ্য বিন্দুতে (উপরের চিত্রটি দেখি) \sqrt 5 একক দৈর্ঘ্যের অতিভুজের উপর ২ একক দৈর্ঘ্যের আরেকটি লম্ব আঁকি। তারপর শুন্যের বিন্দু (শুন্য অবস্থিত যে বিন্ধুতে) এবং নতুন অঙ্কিত লম্বের শীর্ষবিন্দু যোগ করি, তাহলে আমরা আরেকটি সমকোণী ত্রিভুজ পেলাম যার ভুমি হল \sqrt 5 একক এবং লম্ব হল ২ একক। তাহলে আবারো গুরু পীথাগোরাসকে স্বরণ করি। তাঁর উপপাদ্য অনুসারে আমরা জানি, কোনো সমকোণী ত্রিভুজের, অতিভুজ2 = লম্ব2 + ভুমি2 ।
তাহলে উপরের নতুন অঙ্কিত সমকোণী ত্রিভুজটির ক্ষেত্রে,
অতিভুজ2 = (\sqrt 5)2 + 22
বা, অতিভুজ2 = 5 + 4
বা, অতিভুজ2 = 9
বা, অতিভুজ = \sqrt 9 বা 3
তাহলে উপরের নতুন অঙ্কিত সমকোণী ত্রিভুজটির অতিভুজ পেলাম \sqrt 9 একক। অর্থাৎ অতিভুজটির দৈর্ঘ্য পেলাম \sqrt 9। এখন তাহলে আগের মতই অতিভুজটির এক প্রান্ত শূণ্যের উপর ধরে (সংখ্যারেখার উপর যেখানটাই শুন্য অবস্থিত) অতিভুজটিকে সংখ্যারেখার উপর রাখলে তার অন্য প্রান্ত যে বিন্দুতে শেষ হয় শুন্য থেকে ঐ বিন্দু পর্যন্ত দূরত্বই হল আমাদের কাঙ্খিত \sqrt 9 একক দূরত্ব। তাহলে শুন্যকে কেন্দ্র করে নতুন অঙ্কিত ত্রিভুজটির অতিভুজটিকে ব্যাসার্ধ ধরে শুন্য থেকে ডানদিকে (কারন ধনাত্নক সংখ্যাগুলো শুন্য থেকে ডানদিকে অবস্থিত) সংখ্যারেখার উপর একটি বৃত্তচাপ আঁকি। বৃত্তচাপটি সংখ্যারেখার ঠিক যে বিন্দুর উপর দিয়ে যায় ঠিক ঐ বিন্দুটাই হল \sqrt 9 এর ঠিকানা। উপরের চিত্র থেকে দেখা যাচ্ছে \sqrt 9 এর ঠিকানা ৩ যে বিন্দুতে অবস্থিত ঠিক তার উপর। তারমানে আমরা \sqrt 2, \sqrt 3, \sqrt 5 সবার অবস্থান ঠিক ঠিক ভাবে নির্ণয় করতে সক্ষম হয়েছি। (Yahooooo...)
\sqrt 2, \sqrt 3, \sqrt 5:
এখন আমরা \sqrt 2, \sqrt 3, \sqrt 5 সবাইকে একটা সংখ্যারেখার উপর এঁকে দেখি মানের ভিত্তিতে তাদের সবার স্থান ঠিক ঠিক বিন্দুতে নির্ণয় করতে পেরেছি কিনা (আঁকার গড়মিলের জন্য অবস্থান কিছু এদিক ওদিক হলে কর্তৃপক্ষ দায়ী নহে😀):
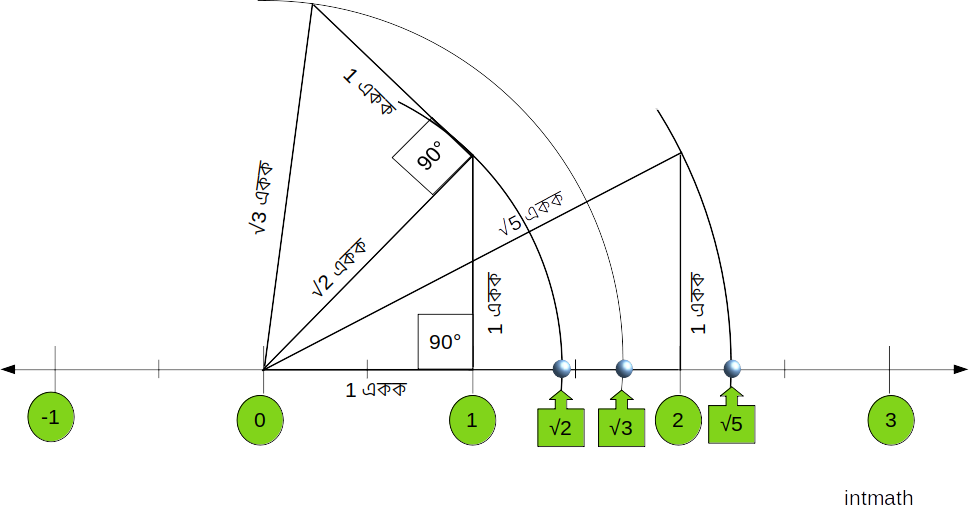
এতক্ষন যাদেরকে দেখলাম তারা তো algebraic number তাই নানা রকম কারসাজি করে সংখ্যা রেখার উপর তাদের অবস্থান গুলো দেখতে পারলাম, কিন্তু "পাই" তো non-algebraic number তাহলে সংখ্যারেখার উপর তার অবস্থান কিভাবে নির্নয় করব। আচ্ছা পাই এর অবস্থান দেখার জন্য নিচের চিত্র ও বর্ননা মনোযোগ দিয়ে দেখি:
π বা pi:
প্রথমে ১ একক ব্যাসের (2r) একটা বৃত্ত আঁকি তাহলে তার ব্যাসার্ধ হবে, r = \frac {১} {২} একক।
আমরা জানি, বৃত্তের পরিধি = 2πr
তাহলে,
বৃত্তের পরিধি = 2πr
= 2\cdotπ\cdot\frac {1} {2}
= π
অর্থাৎ বৃত্তের পরিধি = π, তারমানে \frac {1} {2} একক ব্যাসার্ধের বৃত্তের পরিধি যতখানি আমাদের ভালোবাসার π এর মানও ততখানি।
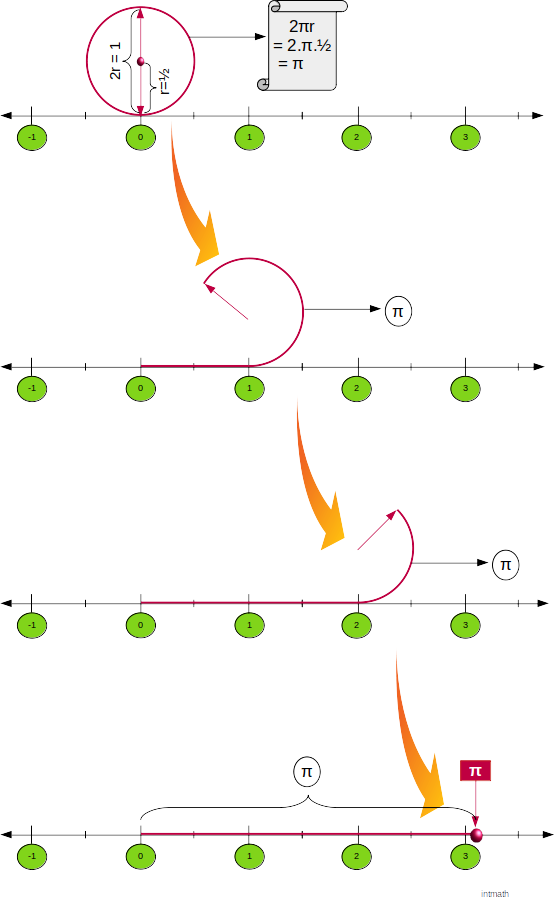
এখন, উপরে বর্ণিত \frac {1} {2} একক ব্যাসার্ধের বৃত্তের পরিধির সমান দৈর্ঘ্যের একটা সুতা নিই ( সুতাটার দৈর্ঘ্যই কিন্তু π এর মান, কারন π = বৃত্তটির পরিধি = সুতার দৈর্ঘ্য)। এখন সুতাটির এক মাথা শুন্যের উপর (সংখ্যারেখার উপর যে বিন্দুতে শুন্যের অবস্থান) রেখে সংখ্যারেখার উপর সুতাটিকে সোজা করে ধরলে সুতাটির শেষ মাথা যে বিন্দুর উপর পড়ে ঐ বিন্দুই হল π এর অবস্থান।
এখন তাহলে আমার কথাটি ফুরোলো নটে গাছটি মুড়োলো।😀😀


Outstanding explanation
Sohoj… sabolil