Complex Number এর বাংলা অর্থ হলো জটিল সংখ্যা, তো নাম দেখেই আমরা বুঝতেছি এরা খুবই জটিল টাইপের (জটিইল্লা) সংখ্যা। আসলে এমন জটিল কিছু না (মানে এখানে যতটুকু আলোচনা হবে আর কি), এই লেখাটা পূর্ণ মনোযোগ দিয়ে পড়লেই জটিল সংখ্যা পানির মত সহজ হয়ে যাবে।
তো জটিল সংখ্যা জানার জন্য আমাদের আরেক ধরনের সংখ্যা সম্পর্কে জানতে হবে যার নাম imaginary number বা কাল্পনিক সংখ্য। মূলত জটিল সংখ্যা দুই ধরনের সংখ্যার সমন্বয়ে গঠিত হয় তার একটি হলো বাস্তব সংখ্যা (যা আমরা সবাই চিনি) আর অন্যটা হলো অবাস্তব বা কাল্পনিক সংখ্যা (এটা নিয়ে একটু পরেই আলোচনা হবে)।
আচ্ছা
:-“কাল্পনিক সংখ্যা” নামটা শুনে প্রথমেই কি মনে হচ্ছে?
:: কল্পনা করে নিতে হয় এমন সব সংখ্যা?
:- হুম আসলেই তাই, বাস্তব অস্তিত্ত্ব নেই জন্য যেসকল সংখ্যাদেরকে কল্পনা করে নিতে হয় (আসলে একটা কাল্পনিক একক যুক্ত করে নিতে হয়) তাদেরকে আমরা কাল্পনিক সংখ্যা বলতে পারি। ব্যপারটা আরো খুলে বলতেছি।
আমরা তো যেকোনো ধনাত্নক পূর্ণ সংখ্যা বা ভগ্নাংশকে বর্গমূল, ঘনমূল বা আরো কোনো মূল করলে মূলদ অথবা অমূলদ সংখ্যা পাই। যেমন,
\begin{aligned} \sqrt{4} &= \sqrt{2\times 2} \\ &= \sqrt{2^2} \\ &= (2^2)^\frac{1}{2} \\ &= 2 \end{aligned}
\begin{aligned} \sqrt{9} &= \sqrt{3\times 3} \\ &= \sqrt{3^2} \\ &= (3^2)^\frac{1}{2} \\ &= 3 \end{aligned}
\begin{aligned} \sqrt[3] 8 &= \sqrt[3]{2\times 2\times 2} \\ &= \sqrt[3]{2^3} \\ &=(2^3)^\frac {1} {3} \\ &= 2 \end{aligned}
\begin{aligned} \sqrt[4] 81 &= \sqrt[4]{3\times 3\times 3\times 3} \\ &= \sqrt[4]{3^4} \\ &= (3^4)^\frac {1} {4} \\ &= 3 \end{aligned}
এভাবে ধনাত্নক পূর্ণ সংখ্যা বা ভগ্নাংশদেরকে বর্গমূল, ঘনমূল, চতুর্মূল, পঞ্চমূল বা আরো কোনো মূল করলে যে মূলদ অথবা অমূলদ সংখ্যা পাওয়া যায় তা আমরা সবাই অলরেডি জানি। এখানে আলোচনার সুবিধার জন্য পূর্ণবর্গ, পূর্ণঘন এরকম সংখ্যা নেওয়া হয়েছে, তবে অন্যান্য সংখ্যা নিয়ে করলেও হবে।
এদেরকে
X^2 - 4 = 0
X^2 -9 = 0
X^3 - 8 = 0
X^4 -81 = 0
সমীকরন গুলো সমাধান করে X এর মান বা মূল হিসেবেও পাওয়া যায়। এখানে আলোচনা টা কে যথাসম্ভব সহজ করবার নিমিত্তে কর্তৃপক্ষ জটিল সমীকরন গুলোকে এড়ানোর চেষ্টা করতেছে)
কিন্তু ঋণাত্নক সংখ্যার ক্ষেত্রে ঘটনাগুলো কি ঘটবে তা জানার জন্য নিচের ঘটনাগুলো দেখি:
এখন আমরা নিচের সমীকরনটি সমাধান করে দেখি কি পাওয়া যায়:
:: 🙄🙄 একটু আগেই না বোল্লা সমীকরন টমীকরন এড়ানোর চেষ্টা করতাছো?
:- ইয়ে মানে… … গণিত করতে গেলে তো ইট্টু আধটু সমীকরন দেখাই লাগে, তাছাড়া এগুলো মোটেই জটিল না খুবই সহজ সমীকরন !!
:: আচ্ছাহ
আচ্ছা এখন তাহলে দেখি:
\begin{aligned}
X^2 + 4 &= 0 \\
⇒ X^2 &= -4 \\
⇒ X &= \sqrt{-4} \\
⇒ X &= \sqrt{4\times (-1)} \\
⇒ X &= 2\sqrt{-1}
\end{aligned}
তার মানে দাঁড়ালো :
\begin{aligned}
\sqrt{-4} &= \sqrt{4\times (-1)} \\
&= 2\sqrt{-1}
\end{aligned}
ঠিক একইভাবে,
\begin{aligned}
\sqrt{-9} &= \sqrt{9\times {(-1)}} \\
&= 3\sqrt{-1}
\end{aligned}
এখানে যে 2, 3 এদের সাথে \sqrt{-1} আসতেছে, এই negative 1 এর বর্গমূলই হল imaginary number বা কাল্পনিক সংখ্যা। imaginary এর i দিয়ে এসব সংখ্যাকে প্রকাশ করা হয়, যেখানে i কোনো সংখ্যার কাল্পনিক অংশকে নির্দেশ করে যিনি iota নামেও পরিচিত। অর্থাৎ
i = \sqrt{-1}। তাহলে,
2\sqrt{-1} = 2i
3\sqrt{-1} = 3i
এই i, 2i, 3i অর্থাৎ i এর সাথে বাস্তব সংখ্যা গুন আকারে থাকলে তাদেরকে pure imaginary number বলা হয়। আর যখন pure imaginary number এর সাথে বাস্তব সংখ্যা যোগ বা বিয়োগ হয়ে জটিল আকার ধারন করে তখন তাদেরকে complex number বলা হয়। সমস্ত complex number এর সেটকে C দিয়ে প্রকাশ করা হয়।
যেমন, 3 + 2i, 2 – 5i, -5 – 2i, 0 + 2i, 3 + 0i ইত্যাদি। তাহলে দেখা যাচ্ছে, এদেরকে আমরা a + bi আকারে লিখতে পারি, যেখানে a বাস্তব অংশ আর b কাল্পনিক অংশ। যদিও a, b উভয়ই বাস্তব সংখ্যা কিন্তু b-র সাথে i থাকলে b কাল্পনিক অংশ হয়ে যায় (অংশ আর সংখ্যা নিশ্চয়ই এক জিনিস না) যেমন, a = 5 হলে a নির্দেশ করে বাস্তব অক্ষ বরাবর (x অক্ষ বরাবর) ধনাত্নক দিকের (শুন্য থেকে ডান দিকে) ৫ ঘর আর bi = 4 হলে বোঝা যায় কাল্পনিক অক্ষ বরাবর (y অক্ষ বরাবর, b এর সাথের i কাল্পনিক অক্ষকে বা y অক্ষকে নির্দেশ করে) ধনাত্নক দিকের (শুন্য থেকে উপরের দিকে) ৪ ঘর।
আচ্ছা, এখন আমরা বুঝলাম যে, একটা বাস্তব ও একটা কাল্পনিক অংশ সংযুক্ত বা বিযুক্ত হয়ে যে a + bi আকারের সংখ্যা গঠন করে তাকে জটিল সংখ্যা বলে। তাহলে যেকোনো জটিল সংখ্যা z = a + bi হলে, বাস্তব অংশ a কে প্রকাশ করা হয় Re(z) (Real part of z) এবং কাল্পনিক অংশ b কে প্রকাশ করা হয় Im(z) (Imaginary part of z) দিয়ে অর্থাৎ z = 3 + 2i হলে Re(z) = 3 এবং Im(z) = 2, এই Re(z) = 3, x অক্ষ বরাবর এবং Im(z) = 2, y অক্ষ বরাবর অবস্থানকে নির্দেশ করে এবং ফাইনালি এই দুই অক্ষের সম্বিলিত প্রচেষ্টার ফলাফল হিসেবে আমরা জটিল সংখ্যার অবস্থান পাই।
তাহলে আমরা বুঝলাম, i = \sqrt{-1}
এখন আমরা i এর বিভিন্ন ঘাত বা পাওয়ারের মান দেখি:
:: oww wait wait wait….
:- yes yes yes?
:: সবই তো বুঝলাম কিন্তু তুমি যে বোল্লা 3 + 0i জটিল সংখ্যা তার মানে কি
:- হা ঠিকই আছে
:: ক্যমনে ঠিক থাকে, 3 + 0i = 3 + 0 = 3; আর 3 তো একটা খাঁটি বাস্তব সংখ্যা আর 0 + 2i ই বা জটিল হয় ক্যামনে আমারে ইট্টু বুঝায়ে কও। 0 + 2i = 2i তার তো pure imaginary হওয়ার কথা।
:- হুম শুনো বলি..
আমরা জটিল সংখ্যার সংগা থেকে কি পেয়েছি:
বাস্তব সংখ্যা \pm কাল্পনিক সংখ্যা = জটিল সংখ্যা। তাহলে 0 + 2i এখানে 0 তো টাটকা বাস্তব সংখ্যা আর 2i কাল্পনিক সংখ্যা তো এই বাস্তব 0 আর কাল্পনিক 2i মিলে তো জটিল সংখ্যার সংগা a + bi কে পরিপূর্ণ ভাবে মানতেছে তাহলে 0 + 2i জটিল সংখ্যা হবেনা কেন!?
:: কিন্তু তাও আমার কেমন জানি খটকা খটকা লাগছে
:- হুম লাগছে কারন আমরা আগেই সংখ্যদেরকে বাস্তব আর কাল্পনিক এই দুই ভাগে ভাগ করে ফেলি। কিন্তু যদি সমস্ত সংখ্যদেরকে আগেই জটিল সংখ্যা ধরে নিয়ে তারপর সেই জটিল সংখ্যাকে বাস্তব আর কাল্পনিক এই দুই প্রকারে ভাগ করতাম তাহলে আর কোনো সমস্যায় পড়া লাগতো না।
:: বুঝছি তারমানে 0 + 2i, 3 + 0i এরা জটিল সংখ্যা। তাহলে শুধু 2i কি হবে আর শুধু 3ই বা কি হবে?
:- শুধু 2i কে pure imaginary আর শুধু 3 কে বাস্তব সংখ্যা বলা যায় কিন্তু আসলে সবাই তো জটিল সংখ্যা। কারন 3 এর সাথে তো 0i প্লাস বা মাইনাস হিসেবে থাকতে পারে আবার 2i এর সাথেও 0 প্লাস বা মাইনাস হিসেবে থাকতে পারে।
:: আচ্ছাহ বুঝলুম।
আচ্ছা এখন তাহলে i এর পাওয়ার বা ঘাত নিয়ে কিছু আলোচনা করা যাক:
আমরা জানি, কোনো রাশির পাওয়ার শুন্য হলে তার মান ১ হয় আর কোনো রাশির পাওয়ার ১ হলে তার মান ঐ রাশি নিজেই হয়, যেমন, x^0 = 1, x^1 = x; একইভাবে, i^0 = 1, i^1 = i;
তাহলে,
\begin{aligned} i^2 &= i\cdot i \\ &= \sqrt{-1}\cdot\sqrt{-1} \\ &= -1 \end{aligned}
\begin{aligned} i^3 &= i^2\cdot i \\ &= -1 \cdot i \\ &= -i \end{aligned}
\begin{aligned} i^4 &= i^3 \cdot i \\ &= -i \cdot i \\ &= -i^2 \\ &= -(-1) \\ &= 1 \end{aligned}
\begin{aligned} i^5 &= i^4\cdot i \\ &= 1\cdot i \\ &= i \end{aligned}
\begin{aligned} i^6 &= i^5 \cdot i \\ &= i \cdot i \\ &= i\cdot 2 \\ &= -1 \end{aligned}
\begin{aligned} i^7 &= i^6 \cdot i \\ &= -1\cdot i \\ &= -i\\ \end{aligned}
\begin{aligned} i^8 &= i^7\cdot i \\ &= -i \cdot i \\ &= -i^2 \\ &= - (-1)\\ &= 1\\ \end{aligned}
দেখা যাচ্ছে যে, মানগুলো একটা সাইকেল বা চক্রাকারে ঘুরতেছে, যেমন, i এর পাওয়ার ১, ২, ৩, ৪ এর জন্য আমরা মান পেয়েছি যথাক্রমে i, -1, -i, 1 (এগুলো কেন এবং কিভাবে হচ্ছে সেসব গ্রাফে এঁকে এঁকে বিস্তারিত দেখব) আবার i এর পাওয়ার ৫, ৬, ৭, ৮ এর জন্যও মান পেয়েছি যথাক্রমে i, -1, -i, 1 এভাবে আমরা হিসাব করলে দেখতে পাবো ৯, ১০, ১১, ১২ এর জন্য আবারো যথাক্রমে i, -1, -i, 1 পাবো (বিশ্বাস না হলে নিজেরা ট্রাই করে দেখতে পারো)। এখান থেকে একটা ট্রিক খুঁজে পেলেই আমরা i এর যেকোনো পাওয়ারের মান সহজেই নির্নয় করতে পারি। ট্রিকটা হল: এখানে আমরা দেখতে পাচ্ছি i এর পাওয়ার বা শক্তি ৪ এর গুনিতক হলেই তার মান ১ হয়ে যাচ্ছে। এখন তাহলে আমরা i এর যেকোনো ঘাতের মান সহজেই নির্নয় করতে পারব। যেমন,
আমরা জানি,
\begin{aligned}
i^4 &= i^2 \cdot i^2\\
&= (-1) \cdot (-1)\\
&= 1\\
\end{aligned}
তাহলে,
\begin{aligned}
i^{28} &= (i^4)^7\\
&= 1^7\\
&= 1\\
\end{aligned}
আবার,
\begin{aligned}
i^{66} &= i^{(4.16+2)}\\
&= (i^4)^{16} \cdot i^2\\
&= {1}^{16} \cdot (-1)\\
&= {1} \cdot (-1)\\
&= -1\\
\end{aligned}
ওকেই এখন আমরা একটা লম্বা ধারা দেখি,
1 + i + i2 + i3 + i4 + i5 + i6 + … … … … + i100 এই ধারার সমষ্টি কত হবে? যেহেতু 1 = i0 সুতরাং ধারাটি আমরা
i0 + i1 + i2 + i3 + i4 + i5 + i6+ … … … … + i100 এভাবে লিখতে পারি।
আচ্ছা বিষয়টা এবার একটু ভেঙ্গে ভেঙ্গে চিন্তা করি:
একটু আগেই শিখে আসলাম i^0 = 1, i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1, i^5 = i এভাবে ক্রমিক পাওয়ারের জন্য মানগুলো চক্রাকারে রিপিট করে, আরো শিখেছি যে প্রতি ৪টা ক্রমিক পাওয়ারের জন্য মানগুলো রিপিট করতেছে। তাহলে আমাদের ধারাটির ২য় পদ (হিসাবের সুবিধার জন্য ১ম পদকে আপাতত বাদ রাখতেছি) থেকে শুরু করে পরপর চারটি পদের সমষ্টি আসে:
i1 + i2 + i3 + i4 = i + (-1) + (-i) + 1
= i – 1 – i + 1
= 0
এখন i4 এর পরবর্তী চারটি পদের সমষ্টি আসে:
i5 + i6+ i7 + i8 = i4.i + i4.i2 + i4.i3 + i4.i4
= i + i2 + i3 + 1
= i + (-1) + (-i) + 1
= i – 1 – i + 1
= 0
আবার i8 এর পরবর্তী চারটি পদের সমষ্টি আসে:
i9 + i10+ i11 + i12 = (i4)2.i + (i4)2.i2 + (i4)2.i3 + (i4)3
= i + i2 + i3 + 1
= i + (-1) + (-i) + 1
= i – 1 – i + 1
= 0
তাহলে আমরা দেখতে পাচ্ছি i এর প্রতি ৪টি ক্রমিক পাওয়ারের জন্য সমষ্টি আসতেছে শুন্য।
এখানে আরো একটা খেয়ালযোগ্য ব্যপার হল: এখানে প্রতি ৪টা পদের প্রথম পদটির i এর পাওয়ার চারের গুনিতকের পরের সংখ্যাটি।
যেমন,
i1 এখানে 1 হল 4*0+1; আবার
i5 এখানে 5 হল 4*1+1; আবার
i9 এখানে 9 হল 4*2+1;
তাহলে যেকোনো ধারার i এর পাওয়ার চারের গুনিতকের পরের সংখ্যা আছে এমন যেকোনো পদ থেকে শুরু করে i এর পাওয়ার চারের গুনিতক আছে এমন যেকোনো পদ পর্যন্ত সকল পদের সমষ্টি হবে 0।
তারমানে i এর পাওয়ার ১ থেকে শুরু করে ৪ এর যেকোনো গুনিতক পর্যন্ত হলেই তাদের সবার মানের সমষ্টি শুন্য হয়ে যাচ্ছে। তারমানে
i1 + i2 + i3 + i4 + i5 + i6+ i7 + i8 + i9 + i10+ i11 + i12 = 0,
i1 + i2 + i3 + i4 + i5 + i6+ i7 + … … … + i23 + i24 = 0,
i1 + i2 + i3 + i4 + i5 + i6+ i7 + … … … + i99 + i100 = 0 তাহলে
i0 + i1 + i2 + i3 + i4 + i5 + i6+ i7 + … … … + i99 + i100
= i0 + 0
= 1 + 0
= 1
অতএব, i0 + i1 + i2 + i3 + i4 + i5 + i6+ i7 + … … … + i99 + i100 = 1;
এখন আমরা সহজেই
i1 + i2 + i3 + i4 + i5 + i6+ i7 + … … … + i2021 এর মানও নির্নয় করতে পারব।
এখানে,
2021 / 4 = 505;
তারমানে i এর পাওয়ার ১ থেকে শুরু করে 505 * 4 = 2020 পর্যন্ত সবগুলো পদের সমষ্টি হবে 0 তাহলে
i1 + i2 + i3 + i4 + i5 + i6+ i7 + … … … + i2021
= 0 + i2021
= (i4)505.i
= 1.i
= i
অতএব,
i1 + i2 + i3 + i4 + i5 + i6+ i7 + … … … + i2021 = i;
এখানে শেষপদের হিসাবটা আমরা আরো সহজে করতে পারি, যেমন: 2021 কে 4 দিয়ে ভাগ করার পর যত অবশিষ্ট থাকে i এর পাওয়ার 4 এর গুনিতক হওয়ার পরে আরো অতগুলো i অবশিষ্ট থাকে। যেমন,
2021 % 4 = 1; অর্থাৎ
i2021 = i2020.i = i আবার
i4023 এখানে 4023%4 = 3, তাহলে
i4023 = i4020.i3 = -i;
সবই তো বুঝলাম কিন্তু
i10+ i11 + i12+ … … … + i500 + i501 এর সমষ্টি কত হবে?
এখানে
i10+ i11 + i12+ … … … + i500 + i501
= i9 + i10+ i11 + i12+ … … … + i500 + i501 – i9
= 0 + i501 – i9
= i500.i – i8.i
= i – i
= 0
অতএব, i10+ i11 + i12+ … … … + i500 + i501 = 0;
আবার,
i10+ i11 + i12+ … … … + i500 = কত?
এখানে,
i10+ i11 + i12+ … … … + i500
= i9 + i10+ i11 + i12+ … … … + i500 – i9
= 0 – i9
= -i8.i
= -i
অতএব, i10+ i11 + i12+ … … … + i500 = -i;
কিন্তু আমার মনে একটা প্রশ্ন আছে, এসব ঋণাত্নক সংখ্যার শুধুমাত্র বর্গমূল করলেই কি কাল্পনিক সংখ্যা পাবো? ঘনমূল, চতু্র্মূল, পঞ্চমূল এসব করলে কি পাবো? ওকেই নিচে সংক্ষিপ্ত ভাবে দেখা যাক কি পাওয়া যায়:
\begin{aligned}
\sqrt[3] {-8} &= \sqrt[3]{8\times (-1)} \\
&= 2\times \sqrt[3]{-1} \\
&= 2\times (-1) {\footnotesize \quad \text{// -1 এর ঘনমূল করলে -1 ই পাওয়া যায়।}} \\
&= -2
\end{aligned}
// -1 এর ঘনমূল, পঞ্চমূল বা আরো কোনো বিজোড় সংখ্যাক মূল করলে -1 ই পাওয়া যায়। সাথে অবশ্য আরো কিছু জটিল টাইপের হাবিজাবি জিনিস পত্র ওয়ালা মূল পাওয়া যায় সেসব নিয়ে এখানে আলোচনা হবেনা।
আবার, ঘনমূল এর ব্যাখ্যাটা এভাবেও করা যায় (যদিও এই ব্যাখ্যাটা বেশি ভাল না মানে স্ট্যান্ডার্ড না আর কি):
\begin{aligned} \sqrt[3] {-27} &= \sqrt[3]{(-3)\times (-3)\times (-3)}\\ &=\sqrt[3]{(-3)^3}\\ &=((-3)^3)^\frac {1} {3}\\ &= {-3}\\ \end{aligned}
এখন হাল্কা করে দেখি এই নিয়ম স্ট্যান্ডার্ড না কেন:
আমরা জানি, \sqrt{9} = {3}
কিন্তু
\begin{aligned}
\sqrt{9} &= \sqrt{(-3)\times (-3)}\\
&= \sqrt{(-3)^2}\\
&= ((-3)^2)^\frac {1} {2}\\
&= {-3}\\
\end{aligned}
অর্থাৎ 3 = {-3}
এখানে নিন্দুকেরা বলবে \sqrt{9} তো \pm 3, তাহলে 3 = {-3} না ঠিকই কিন্তু \sqrt{9} = {-3} এটাও তো সত্য। তাদের জন্য নিচের ঘটনাটা দেখি:
\begin{aligned}
{-1} &= {i^2}\\
&= i \times i\\
&= \sqrt{-1}\times \sqrt{-1}\\
&= \sqrt{(-1)\times (-1)}\\
&= \sqrt{1}\\
&= 1\\
\end{aligned}
অর্থাৎ {-1} = {1} এখন নিশ্চয়ই সবাই বলবে আজব তো!! ১ আর -১ সমান হয় নাকি!!! হুমম এখানে একটা ঘাপলা আছে। ঘাপলাটা ম্যাথমেটিশিয়ানদের স্ব স্ব অনুসন্ধানের উপর ছেড়ে দেওয়া হল।
এখন দেখি চতুর্মূল, পঞ্চমূল করলে কি পাওয়া যায়:
\begin{aligned} \sqrt[4] {-16} &= \sqrt[4]{16\times (-1)}\\ &= 2\times \sqrt[4]{-1}\\ &= 2\times (-1)\\ &= -2\\ \end{aligned}
\begin{aligned} \sqrt[5] {-32} &= \sqrt[3]{(-2)\times (-2)\times (-2)\times (-2)\times (-2) }\\ &= \sqrt[5]{(-2)^5}\\ &=((-2)^5)^\frac {1} {5}\\ &= {-2}\\ \end{aligned}
তাহলে দেখা যাচ্ছে ঋণাত্নক সংখ্যার ঘনমূল করলে অলওয়েজ ঋণাত্নক সংখ্যা পাওয়া যাচ্ছে (আসলে আরো দুইটা জটিল মূল পাওয়া যায়) যেমন, \sqrt[3]{-1} এর ক্ষেত্রে −1 ছাড়াও (12+i3\sqrt2) এবং (12−i3\sqrt2) পাওয়া যায়।
তাহলে i সম্বলিত বা সংযোজিত সংখ্যাদেরকে আমরা imaginary number বা কাল্পনিক সংখ্যা বলতেছি আর বাস্তব ও কাল্পনিক সংখ্যার সমন্বয়ে গঠিত a+bi আকারের সংখ্যা গুলো হল জটিল সংখ্যা। অন্যভাবে বলা যায়: যে সকল সংখ্যাকে সংখ্যারেখার (বাস্তব সংখ্যাদেরকে শুধুমাত্র x অক্ষ বরাবার যে একমাত্রিক রেখার উপর দেখানো হয়) সাহায্যে দেখানো যায়না কিন্তু y অক্ষের সাহায্য নিয়ে গ্রাফের মাধ্যমে অবস্থান নির্দিষ্ট করা যায় তাদেরকে জটিল সংখ্যা বলা হয়। অর্থাৎ যেহেতু জটিল সংখ্যার দুইটা পার্ট থাকে তাই এদেরকে প্রকাশ করার জন্য দুইটা অক্ষরেখার প্রয়োজন হয় তার একটা হল x অক্ষ বরাবর বাস্তব অংশ এবং অন্যটা হল y অক্ষ বরাবর অবাস্তব বা কাল্পনিক অংশ। অর্থাৎ জটিল সংখ্যাকে সংখ্যারেখার উপর জায়গা দেওয়া না গেলেও লেখচিত্র বা গ্রাফের মাধ্যমে সহজেই তাদের অবস্থান সঠিক ভাবে দেখানো যায়। নিচের চিত্রটি মনোযোগ দিয়ে দেখলে বিষয়টা আরো ক্লিয়ার হবে।
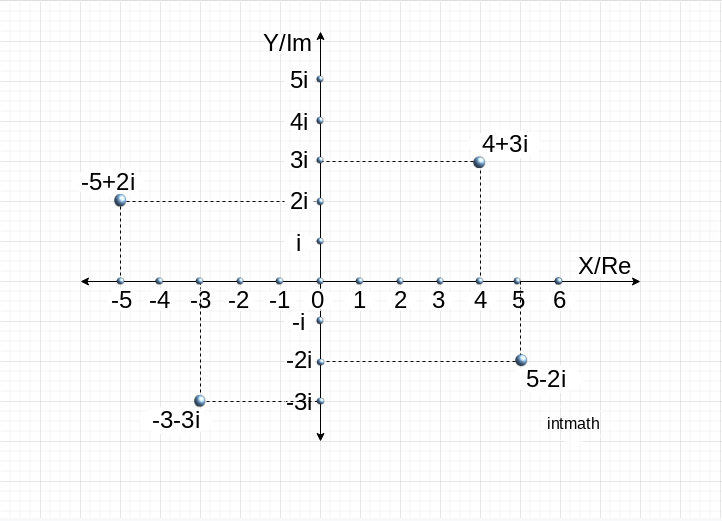
এখানে x অক্ষ বরাবর সকল বাস্তব সংখ্যা ও y অক্ষ বরাবর সকল কাল্পনিক সংখ্যা নিয়ে জটিল সংখ্যার অবস্থান দেখানো হয়েছে। দেখা যাচ্ছে 4+3i এর অবস্থান ১ম চতুর্ভাগে (শুণ্য থেকে ডানে এবং x অক্ষ থেকে উপরের দিকে) কারন 4+3i এর বাস্তব অংশ 4, x অক্ষের উপর শুণ্য থেকে ডান দিকের ৪র্থ বিন্দুতে (পূর্ণ সংখ্যাগুলো যে সকল বিন্দুতে অবস্থিত) অবস্থিত এবং কাল্পনিক অংশ 3i, y অক্ষের উপর শুণ্য থেকে উপরের দিকের ৩য় বিন্দুতে অবস্থিত। একইভাবে -5+2i এর অবস্থান ২য় চতুর্ভাগে (শুণ্য থেকে বামে এবং x অক্ষ থেকে উপরের দিকে) কারন -5+2i এর বাস্তব অংশ -5, x অক্ষের উপর শুণ্য থেকে বাম দিকের ৫ম বিন্দুতে অবস্থিত এবং কাল্পনিক অংশ 2i, y অক্ষের উপর শুণ্য থেকে উপরের দিকের ২য় বিন্দুতে অবস্থিত। একই ভাবে -3-3i ৩য় চতুর্ভাগে এবং 5-2i ৪র্থ চতুর্ভাগে অবস্থিত। তাহলে উপরের গ্রাফ থেকে আমরা দেখতে পাচ্ছি যে complex number আসলে দুই মাত্রার বা দ্বিমাত্রিক নাম্বার।, কেননা তাদের অবস্থান নির্দিষ্ট করার জন্য দুইটা মাত্রার (x ও y) বা অক্ষের প্রয়োজন হচ্ছে।
এখন একটা ইনটারেস্টিং জিনিস দেখি: নিচের চিত্রটি মনোযোগ দিয়ে দেখি :
এখানেও x অক্ষ বরাবর বাস্তব সংখ্যা ও y অক্ষ বরাবর কাল্পনিক সংখ্যা নিয়ে জটিল সংখ্যার ঘূর্ণন নিয়ে সংক্ষিপ্ত আলোচনা হয়েছে।
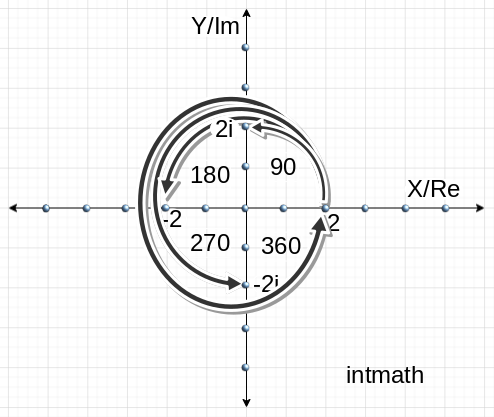
এখানে দেখি 2i0 এর মান কি হয়, আমরা জানি, যখন i এর পাওয়ার শুন্য তখন তার মান ১ অর্থাৎ i0 = 1, অতএব 2i0 = 2*1 = 2 যা বাস্তব সংখ্যারেখার উপর (x অক্ষের উপর) শুণ্য থেকে ডানের ২য় বিন্দুতে অবস্থিত এবং x অক্ষের সাথে শুন্য ডিগ্রী কোন উৎপন্ন করে। আবার i এর পাওয়ার যখন এক তখন তার মান i অর্থাৎ i1 = i অর্থাৎ 2i1 = 2i যা y অক্ষ বরাবর কাল্পনিক সংখ্যারেখার উপর ২য় বিন্দুতে অবস্থিত যা x অক্ষের সাথে 90 ডিগ্রী কোন উৎপন্ন করে আবার i এর পাওয়ার যখন ২ তখন তার মান -১ অর্থাৎ i2 = -1, তাহলে 2i2 = 2*(-1) = -2 যা x অক্ষের উপর ঋণাত্নক দিকের ২য় বিন্দুতে অবস্থিত এবং সে x অক্ষের সাথে 180 ডিগ্রী কোন উৎপন্ন করে একই ভাবে i এর পাওয়ার যখন ৩ তখন তার মান -i অর্থাৎ i3 = -i, তাহলে 2i3 = 2*(-i) = -2i যা y অক্ষের (কাল্পনিক সংখ্যারেখার) উপর ঋণাত্নক দিকের (শুণ্য থেকে নিচের দিকের) ২য় বিন্দুতে অবস্থিত এবং সে x অক্ষের সাথে 270 ডিগ্রী কোন উৎপন্ন করে আবারো একই ভাবে i এর পাওয়ার যখন ৪ তখন তার মান 1 হয়ে যাচ্ছে অর্থাৎ i4 = 1, তাহলে 2i4 = 2*1 = 2 যা x অক্ষের উপর ধণাত্নক দিকের ২য় বিন্দুতে অবস্থিত এবং সে x অক্ষের সাথে 360 ডিগ্রী (মতান্তরে ০ ডিগ্রী) কোন উৎপন্ন করে। তাহলে আমরা দেখতে পাচ্ছি কোনো কিছুকে একবার i দিয়ে গুন করলেই সে তার পুর্বের অবস্থান থেকে ৯০ ডিগ্রী এঙ্গেলে দূরে সরে যাচ্ছে। যেমন, ২ এর অবস্থান ছিলো x অক্ষের উপর তাকে i দিয়ে গুন (2i) করার সাথে সাথেই সে চলে গেল y অক্ষের উপর (নিষ্ঠুর তুমি বড়ই নিষ্ঠুর তুমি) আবার y অক্ষের উপর থাকবি থাক, তা না আবারো i দিয়ে গুন (2i2) করার ফলে সে চলে গেল x অক্ষের ঋণাত্নক দিকে অর্থাৎ এবার সে তার প্রথম অবস্থা থেকে ১৮০ ডিগ্রী এঙ্গেলে দূরে সরে গেল!
এখন দেখি complex number এর যোগ, বিয়োগ, গুন, ভাগ:
যোগ:
মনে করি, দুইটি জটিল সংখ্যা z1 = a + bi ও z2 = c + di
তাহলে, z1 + z2 = ( a + bi ) + (c + di)
= a + bi + c + di
= a + c + bi + di
= (a + c) + (b + d)i
যার বাস্তব অংশ হল (a+c) এবং কাল্পনিক অংশ হল (b+d)i
বিয়োগ:
মনে করি, দুইটি জটিল সংখ্যা z1 = a + bi ও z2 = c+di
তাহলে, z1 – z2 = ( a + bi ) – (c+di)
= a + bi – c – di
= a – c + bi – di
= (a – c) + (b – d)i
যার বাস্তব অংশ (a – c) এবং কাল্পনিক অংশ (b – d)i
গুন:
মনে করি, দুইটি জটিল সংখ্যা z1 = a + bi ও z2 = c+di
তাহলে, z1 * z2 = ( a + bi ) * (c+di)
= a*c + a*di + bi*c + bi*di
= ac + adi + bci + bdi2
= ac + adi + bci + bd(-1)
= ac + adi + bci – bd
= ac – bd + adi + bci
= (ac – bd) + (ad + bc)i
যার বাস্তব অংশ (ac – bd) এবং কাল্পনিক অংশ (ad + bc)i
ভাগ :
মনে করি, দুইটি জটিল সংখ্যা z1 = a + bi ও z2 = c+di
তাহলে, z1 / z2 = ( a + bi ) / (c+di)
=
(চলছে)


