বিভাজ্যতা পর্ব-২

আচ্ছা এই পর্বে আমরা ৩,৯ এর বিভাজ্যতা নিয়ে আলোচনা করব।
বিভাজ্যতা কি, ভাজ্য, ভাজক, ভাগশেষ ইত্যাদি কি সেসব আমরা বিভাজ্যতা পর্ব-১ এ দেখেছি। এখন আমরা সরাসরি মুল আলোচনায় চলে যাই।

৩ দ্বারা বিভাজ্যতা:

আচ্ছা ৩ সংখ্যাটি কোন ধরনের সংখ্যাকে নিঃশেষে ভাগ করে আর কিভাবে করে সেটা দেখার আগে চট করে ৩ এর ঘরের নামতা বা মাল্টিপ্লিকেশন টেবিলটা একটু দেখে আসি:

৩ × ১ = ৩
৩ × ২ = ৬
৩ × ৩ = ৯
৩ × ৪ = ১২
৩ × ৫ = ১৫
৩ × ৬ = ১৮
৩ × ৭ = ২১
৩ × ৮ = ২৪
৩ × ৯= ২৭

এভাবে বাড়তে থাকে। এক অংকের সংখ্যা গুলো কোনো সংখ্যা (৩ / ৪ / ৫ ইত্যাদি) দিয়ে বিভাজ্য কিনা তা আমরা সহজেই বুঝতে পারি।
যেমন: ৩, ৬, ৯ এদেরকে দেখলেই বোঝা যায় যে এরা ৩ দিয়ে নিঃশেষে বিভাজ্য। কিন্তু যে সকল সংখ্যা ১টার বেশি অংক নিয়ে গঠিত তাদের দিকে এখন একটু স্পেশাল দৃষ্টি নিবদ্ধ করা যাক:
উপরের নামতা থেকে দেখতে পাচ্ছি
৩ × ৪ = ১২ এখানে ১২ এর অংক দুটিকে যোগ করলে পাই: ১+২=৩ (যিনি ৩ দ্বারা নিঃশেষে বিভাজ্য)
৩ × ৫ = ১৫ এখানে ১৫ এর অংক দুটিকে যোগ করলে পাই: ১+৫=৬ (ইনিও ৩ দ্বারা নিঃশেষে বিভাজ্য)
৩ × ৬ = ১৮ এখানে ১৮ এর অংক দুটিকে যোগ করলে পাই: ১+৮=৯ (ইনিও ডট ডট ডট)
৩ × ৭ = ২১ এখানে ২১ এর অংক দুটিকে যোগ করলে পাই: ২+১=৩ (ইনিও)
৩ × ৮ = ২৪ এখানে ২৪ এর অংক দুটিকে যোগ করলে পাই: ২+৪=৬ (ইনিও)
অর্থাৎ দেখা যাচ্ছে কোন সংখ্যা যত বড়ই হোক বা যত ছোটই হোক তার অংক গুলোর সমষ্টি ৩ দিয়ে বিভাজ্য হলে ঐ সংখ্যটিও ৩ দিয়ে বিভাজ্য হয়।
এভাবে আমরা দেখতে পাই:
৩ × ৭০ = ২১০ এখানে ২১০ এর অংক ত্রয়কে যোগ করলে পাই: ২+১+0=৩ (এখানে সমষ্টি ৩, ৩ দ্বারা নিঃশেষে বিভাজ্য)
৩ × ২৮১ = ৮৪৩ এখানে ৮৪৩ এর অংক তিনটিকে যোগ করলে পাই: ৮+৪+৩=১৫ আবার ১+৫=৬ যা ৩ দ্বারা নিঃশেষে বিভাজ্য।
অবস্থা যদি এমন হয় যে, যোগফল অনেক বড় হয়ে যাচ্ছে যে ৩ দিয়ে বিভাজ্য কিনা বোঝা যাচ্ছেনা, সেক্ষেত্রে ঐ যোগফলের অংকগুলোকে আবার যোগ করতে হবে।
যেমন:
২৭৬৯৩ এখানে ২+৭+৬+৯+৩=২৭ এবং ২৭ এর ২+৭=৯ যা ৩ দিয়ে বিভাজ্য।
এখন দেখি কারা ৩ দিয়ে বিভাজ্য হবেনা:
৩১০১৩০৩ এখানে ৩+১+০+১+৩+০+৩=১১ এবং ১+১=২ যা ৩ দিয়ে বিভাজ্য নয় সুতরাং ৩১০১৩০৩ ও ৩ দিয়ে বিভাজ্য হবেনা! (বিশ্বাস না হলে নিজেরা ট্রাই করে দেখতে পারো)

:: আচ্ছা সব তো বুঝলাম কিন্তু মনে করো ১০০ ডিজিটের সংখ্যাকে ৩ দিয়ে বিভাজ্য কিনা চেক করতে হবে, তো ১০০ টা ডিজিট প্রথমে যোগ করে তারপর আবার সেই যোগফলের ডিজিট গুলোকে যোগ করে করে এভাবে করা তো অনেক সময়ের ব্যপার।
:- সেক্ষেত্রে প্রতিটা অংক থেকে ৩ বাদ দিয়ে দিয়ে হিসাব করা যায়।
:: বুঝলাম নাহ
:- আচ্ছা, মনে করো ২৩৮৭৮৬৫ একে দেখব ৩ দিয়ে বিভাজ্য কিনা। তো প্রথমে ২ আছে, ২ থেকে তো ৩ বাদ দেয়া যায়না তাই ২কে হাতে রাখলাম। তারপর আছে ৩, ৩ তো ৩ দিয়ে বিভাজ্য তাই ওকে কেটে দিলাম। তারপর আছে ৮, ৮ এর মধ্যে ৬ আছে যে ৩ দিয়ে বিভাজ্য তাই ৮ থেকে ৬ বাদ দিয়ে দিলাম থাকবে ২। এই ২ আর হাতের ২ মিলিয়ে হল ৪, এই ৪ থেকে ৩ বাদ দিলে থাকবে ১, এই ১কে হাতে রাখব। তারপর আছে ৭, ৭ থেকে ৬ বাদ দিলে থাকবে ১, এই ১ আর হাতের ১ মিলিয়ে ২ হবে একে আবার হাতে রাখবো। তারপরে আছে আবার ৮, এই ৮ থেকে ৬ বাদ দিলে থাকবে ২, এই ২ আর হাতের ২ মিলিয়ে হবে ৪, আবার এই ৪ থেকে ৩ বাদ দিয়ে ১ কে হাতে রাখব। তারপর আছে ৬ যা ৩ দিয়ে বিভাজ্য তাই এই ৬ কে বাদ দিয়ে দিবো। তারপর আছে ৫, এই ৫ থেকে ৩ বাদ দিলে থাকবে ২, এই ২ আর আগের হাতের ১ মিলিয়ে ৩ হবে, এই ৩ তো ৩ দিয়ে নিঃশেষে বিভাজ্য তাই ২৩৮৭৮৬৫ সংখ্যাটিও ৩ দিয়ে নিঃশেষে বিভাজ্য।
এভাবে আমরা যেকোনো সংখ্যারই শেষ অংকটি পর্যন্ত ৩ বা তার গুনিতক গুলোকে বাদ দিয়ে দিয়ে অবশিষ্টাংশ যোগ করে সহজেই বুঝতে পারি যে সংখ্যাটি ৩ দিয়ে বিভাজ্য কিনা।
নিচের ছবিটি দেখলে আরো ভালো মতো বোঝা যাবে:
ছবিটা আপাত ভাবে দেখে জটিল মনে হলেও একটু মনোযোগ দিয়ে দেখলেই সহজে বোঝা যাবে যে কি ঘটতেছে:

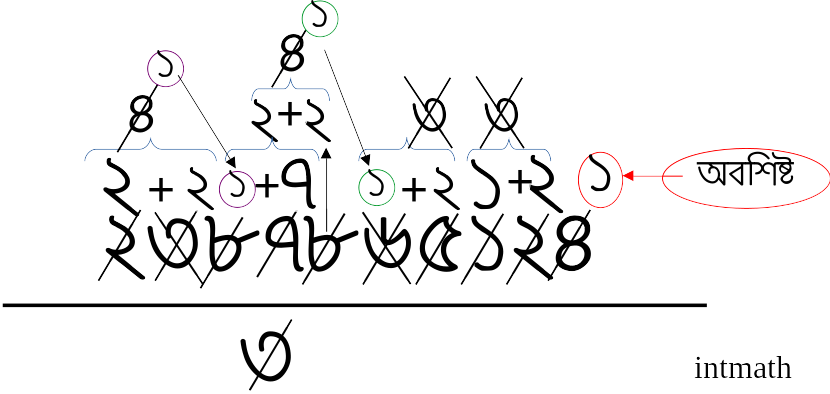
এখানে ২৩৮৭৮৬৫১২৪ সংখ্যাটির সমস্ত কাটাকাটির শেষে ১ অবশিষ্ট আছে যা ৩ দিয়ে বিভাজ্য না, তাই ২৩৮৭৮৬৫১২৪ সংখ্যাটিও ৩ দিয়ে নিঃশেষে বিভাজ্য হবেনা।

এখন দেখি কোনো সংখ্যা ৩ দিয়ে নিঃশেষে বিভাজ্য না হলে ভাগশেষ হিসেবে আমরা কি কি পেতে পারি:
নিচের চিত্রটি দেখি:

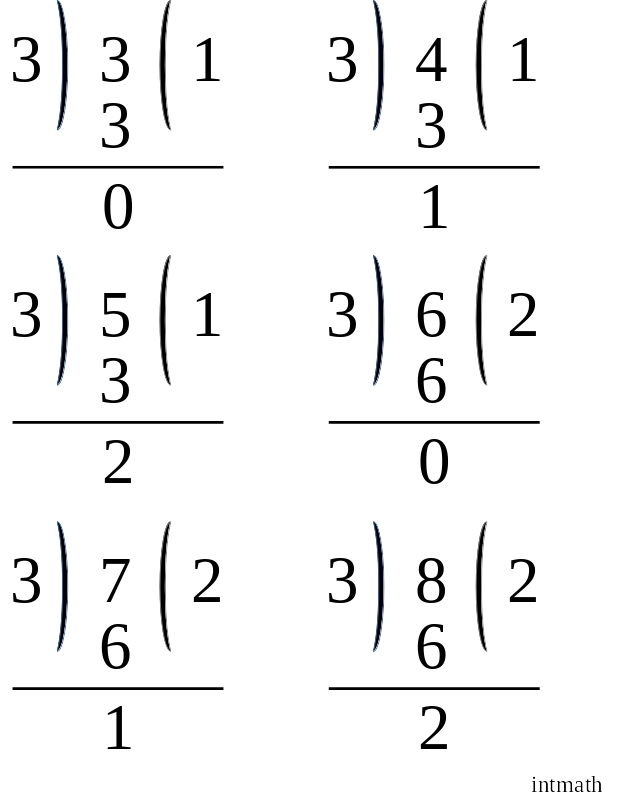
উপরের চিত্র থেকে আমরা দেখতে পাচ্ছি যে, ৩, ৪ ও ৫ কে ৩ দিয়ে ভাগ করলে যথাক্রমে ০, ১ ও ২ অবশিষ্ট থাকে। আবার ৬, ৭, ৮ কে ৩ দিয়ে ভাগ করলে আবারো যথাক্রমে ০, ১ ও ২ ই অবশিষ্ট থাকতেছে।
এখানেও কারো মনে প্রশ্ন আসতে পারে যে, ৩ দিয়ে বিভাজ্যতার সময় ভাগশেষ ৩ বা তার থেকে বড় হয়না কেন? বড় হয়না কেন তা আমরা সবাই জানি তাও সবাই আরেকবার জেনে নিই, বড় হয়না কারন ৩ অবশিষ্ট থাকলে তো ৩ এর মধ্যে ৩ আরো একবার ভাগ যায়। আবার যদি অবশিষ্ট ৪ রাখতে চাই তাও হবেনা কারন ৪ এর মধ্যেও একটা আস্ত ৩ আছে (৩+১=৪) যার জন্য ৩, ৪ এর মধ্যে আরো একবার ভাগ যায় এই কারনে ভাগশেষ কখনই ভাজকের থেকে বড় হয় না।

তাহলে আমরা পেলাম:
১। কোনো সংখ্যার অংক গুলোর সমষ্টি ৩ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ৩ দিয়ে নিঃশেষে বিভাজ্য হবে।
২। কোনো সংখ্যাকে ৩ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০, ১, ২ এর মধ্যে যেকোনো ১টা হবে, এর বাইরে অন্য কিছু হওয়া সম্ভব না (ওই একই কারনে যে ভাগশেষ কখনই ভাজকের থেকে বড় হয় না।)
৩। ৩ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ৩টি ক্রমিক সংখ্যাকে ৩ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে যেমন: উপরের চিত্র থেকে দেখতে পাচ্ছি যে ৩, ৪ ও ৫ কে ৩ দিয়ে ভাগ করলে যথাক্রমে ০, ১ ও ২ ভাগশেষ থাকে। অর্থাৎ ৩ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ৩টি, ০ থেকে ২ পর্যন্ত এবং কোনো একটি সংখ্যাকে ভাগ করলে এই ৩টির থেকে যেকোনো একটি ভাগশেষ পাওয়া যাবে।
৪। পরপর ৩ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে কিনা ৩ দিয়ে নিঃশেষে বিভাজ্য।
৫। কোনো সংখ্যার অংক গুলোর সমষ্টি ৩ দিয়ে নিঃশেষে বিভাজ্য না হলেও ভাগের পর যত অবশিষ্ট থাকে পুরো সংখ্যা টাকেও ৩ দিয়ে ভাগ করলে সেই একই ভাগশেষ পাওয়া যায় (এই বাক্যটাও কর্তৃপক্ষের ব্যক্তিগত মতামত, আপনারা পরীক্ষা-নিরীক্ষা, পর্যবেক্ষণ দ্বারা ভুল প্রমানিত করলে কর্তৃপক্ষকে জানানোর জন্য অনুরোধ জানানো থাকলো)

এখন দেখি ৯ এর বিভাজ্যতা:
৩ এর বিভাজ্যতা বুঝতে পারলে আসলে ৯ এর বিভাজ্যতাও ইতোমধ্যে বোঝা হয়ে গেছে। ৯ এর বিভাজ্যতার ক্ষেত্রেও সংখ্যাটির (যাকে ৯ দিয়ে ভাগ করব) অংক গুলোর সমষ্টি যদি ৯ দিয়ে নিঃশেষে বিভাজ্য হয় তাহলে পুরো সংখ্যাটিই ৯ দিয়ে বিভাজ্য হবে।
কিন্তু কোনো অংকই তো ৯ এর থেকে বড় হওয়া সম্ভব না তাই এক্ষেত্রে ২টা বা ৩টা করে ডিজিট নিয়ে হিসাব করলে সুবিধা হবে।
নিচের ছবিটি মনোযোগ দিয়ে দেখি:

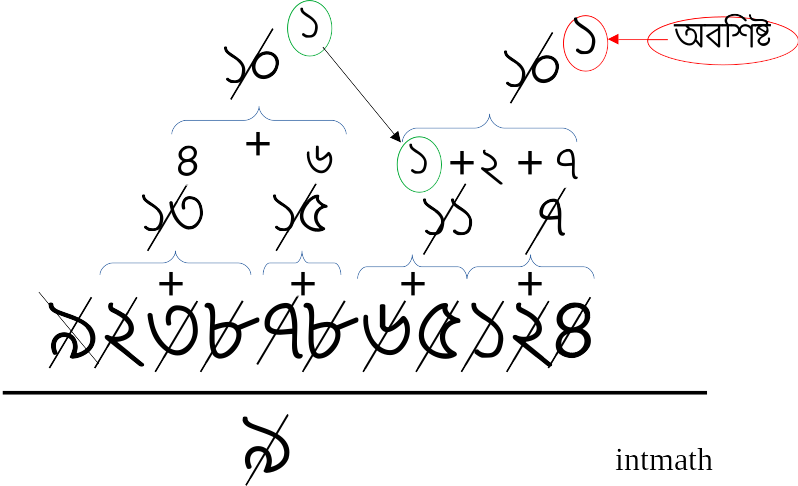
এখানেও ৯২৩৮৭৮৬৫১২৪ এর সব গুলো অংকের সমষ্টিকে ৯ দিয়ে ভাগ করলে সবশেষে ১ অবশিষ্ট থাকে যা ৯ দিয়ে বিভাজ্য না। তাই ৯২৩৮৭৮৬৫১২৪ সংখ্যাটিও ৯ দিয়ে নিঃশেষে বিভাজ্য হবেনা।

এখন দেখি ৯ এর সম্ভাব্য সকল ভাগশেষ:

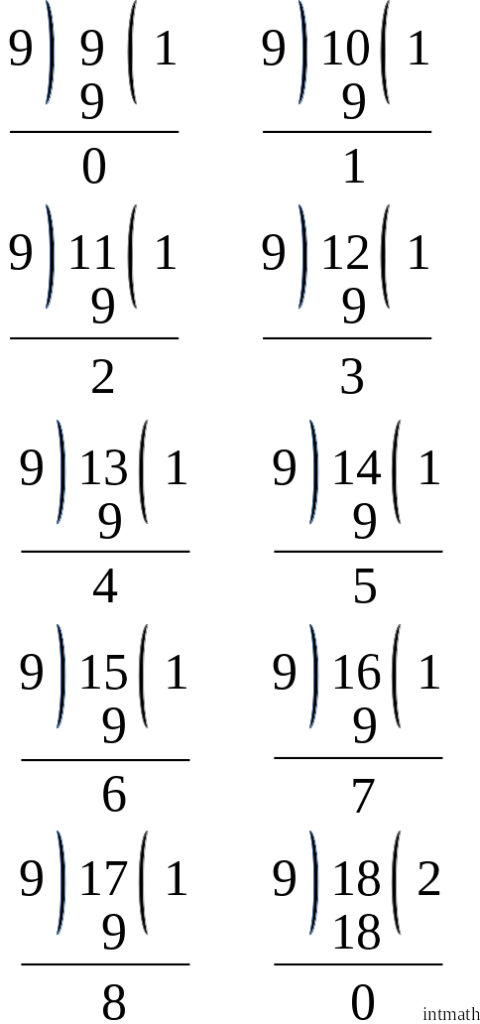
তাহলে আমরা পেলাম:
১। কোনো সংখ্যার অংক গুলোর সমষ্টি ৯ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ৯ দিয়ে নিঃশেষে বিভাজ্য হবে।
২। কোনো সংখ্যাকে ৯ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০, ১, ২, ৩, ৪, ৫, ৬, ৭, ৮ এর মধ্যে যেকোনো ১টা হবে, এর বাইরে অন্য কিছু হওয়া সম্ভব না (ওই একই কারনে ভাগশেষ কখনই ভাজক ৯ এর থেকে বড় হবে না।)
৩। ৯ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ৯টি ক্রমিক সংখ্যাকে ৯ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে যেমন: উপরের চিত্র থেকে দেখতে পাচ্ছি যে ৯, ১০, ১১, ১২, ১৩, ১৪,১৫,১৬ ও ১৭ কে ৯ দিয়ে ভাগ করলে যথাক্রমে ০ থেকে ৮ পর্যন্ত সবগুলো ক্রমিক সংখ্যাকে ভাগশেষ হিসেবে পাওয়া যায়। অর্থাৎ ৯ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ৯টি, ০ থেকে ৮ পর্যন্ত এবং কোনো সংখ্যাকে ৯ দিয়ে ভাগ করলে এই ৯টির থেকে যেকোনো একটি ভাগশেষ আমরা পেয়ে থাকি।
৪। পরপর ৯ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে কিনা ৯ দিয়ে নিঃশেষে বিভাজ্য।
৫। কোনো সংখ্যার অংক গুলোর সমষ্টি ৯ দিয়ে নিঃশেষে বিভাজ্য না হলেও ভাগের পর যত অবশিষ্ট থাকে পুরো সংখ্যা টাকেও ৯ দিয়ে ভাগ করলে সেই একই ভাগশেষ পাওয়া যায় (এই বাক্যটাও কর্তৃপক্ষের ব্যক্তিগত মতামত, আপনারা ভুল প্রমানিত করলে কর্তৃপক্ষকে জানানোর জন্য অনুরোধ জানানো থাকলো)

তো এই হলো বিভাজ্যতা পর্ব-২।