আজকের আলোচনার বিষয়বস্তুু যদিও আমাদের বেশির ভাগেরই জানা আছে তবুও কিছু রিভিউ করা হলো। এখানে ২,৪,৮,১৬ ইত্যাদির বিভাজ্যতার একেবারে basic বিষয়গুলো আলোচনা হবে।
সবার আগে দেখি বিভাজ্যতা কি জিনিস:
বিভাজ্য অর্থ হল বিশেষ ভাবে ভাজ্য বা যাকে বিশেষ ভাবে ভাজা যায়। অর্থাৎ ‘কোনো জিনিস’ (ভাজ্য বা যাকে ভাজা হয়) কে যদি ‘অন্য কোনো জিনিস’ (ভাজক বা যে ভাজে) দিয়ে বিশেষ ভাবে ভাগ করা যায় তাহলে ‘কোনো জিনিস’কে ‘অন্য কোনো জিনিস’ দ্বারা বিভাজ্য বলা হয়। আর ‘বিশেষ ভাবে ভাগ’ বলতে এখানে নিঃশেষে বিভাজ্যতা বোঝানো হয়েছে। অর্থাৎ যে ভাগ প্রকৃয়ার শেষে ভাগশেষ হিসেবে শুন্য থাকে বা কোনো ভাগশেষ থাকেনা তাকে নিঃশেষে বিভাজ্যতা বলে। যেমন, ৯ সংখ্যাটি ৩ দিয়ে বিভাজ্য আবার ২৭, ৯ দিয়ে বিভাজ্য আবার ২৭ কিন্তুু ৯ ও ৩ উভয় দিয়েই বিভাজ্য।
যদিও এসব আমরা ছোটবেলা থেকেই জানি তবুও কিছু গুলু মুলু টাইপের বাচ্চাদের মনে প্রশ্ন আসতে পারে যে, ১০ কে ৩ দিয়ে ভাগ করলে কি তাকে বিভাজ্যতা বলা যাবেনা? উত্তর হলো: বলা যাবে কিন্তু মনে রাখতে হবে ১০, ৩ দিয়ে বিভাজ্য কিন্তু নিঃশেষে বিভাজ্য নয় কেননা ভাগ প্রক্রিয়ার শেষে তখন ভাগশেষ ০ না থেকে ১ থাকে। এখানে অবশ্য নিঃশেষে বিভাজ্য না লিখে শুধু বিভাজ্যই লেখা হবে কেননা বারবার নিঃশেষে বিভাজ্য-নিঃশেষে বিভাজ্য লেখা খুবই কষ্টকর ব্যপার।
এখন নিচের চিত্রটি দেখি:

তাহলে আমরা পেলাম:

এখন আসি আসল কথায়:
আমরা তো সবাই জোড়, বিজোড় সংখ্যা চিনি। আমরা তো numbers থেকে দেখেছি যে, যে সংখ্যাকে সমান দুই ভাগে ভাগ করা যায় সে জোড় সংখ্যা আর যাকে সমান দুই ভাগে ভাগ করা যায়না সে বিজোড়। আরো সহজ কথায় যে সংখ্যার শেষের অংকটি (একক স্থানীয় অংকটি) জোড় সে সংখ্যার পুরোটাই জোড় সংখ্যা যেমন, ২, ১০২, ৭৮৯১২৪ ইত্যাদি আর যে সংখ্যার শেষের অংকটি (একক স্থানীয় অংকটি) বিজোড় সে সংখ্যার পুরোটাই বিজোড় সংখ্যা, যেমন, ৫, ৮৯০৯৭, ৬৭৪০০০৩ ইত্যাদি। যেহেতু জোড় সংখ্যাকে সমান দুই ভাগে ভাগ করা যায় তাহলে সকল জোড় সংখ্যা অবশ্যই ২ দিয়ে নিঃশেষে বিভাজ্য হবে, আর যেহেতু বিজোড় সংখ্যাকে সমান দুই ভাগে ভাগ করা যায়না তাহলে কোনো বিজোড় সংখ্যাই ২ দিয়ে নিঃশেষে বিভাজ্য হবেনা। খুব ভাল কথা, কিন্তু নিঃশেষে বিভাজ্য না হলে কি হবে সেটা দেখি:
২ দ্বারা বিভাজ্যতা:
১১ বিজোড় সংখ্যাটিকে ২ দিয়ে ভাগ করলে আমরা ভাগফল হিসেবে ৫ এবং ভাগশেষ হিসেবে ১ পাই (১১÷২=৫ r=1), এভাবে যেকোনো বিজোড় সংখ্যাকে ২ দিয়ে ভাগ করলে ভাগশেষ হিসেবে সবসময়ই ১ পাবো আর যেকোনো জোড় সংখ্যাকে ২ দিয়ে ভাগ করলে তো ভাগশেষ হিসেবে সবসময়ই ০ পাবো (নিঃশেষে বিভাজ্য হলে তো সব সময়ই ভাগশেষ ০ হয়) তাহলে আমরা বলতে পারি কোনো সংখ্যা যত বড়ই হোক তার শেষ অংকটি ২ দিয়ে নিঃশেষে বিভাজ্য হলে সম্পূর্ণ সংখ্যাটিই ২ দিয়ে নিঃশেষে বিভাজ্য হবে।
তাহলে আমরা পেলাম:
1. যেকোনো জোড় সংখ্যাই ২ দিয়ে নিঃশেষে বিভাজ্য।
2. যেকোনো সংখ্যাকে ২ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০ অথবা ১ এর বাইরে অন্য কিছু হবে না। অর্থাৎ ২ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ২টি।
আবার ক্রমিক সংখ্যাগুলো তো প্রথমে জোড় থাকলে পরেরটা বিজোড় তারপরেরটা আবার জোড় তারপরেরটা আবার বিজোড় এভাবে আসে যেমন: ২,৩,৪,৫ এভাবে, তাহলে আমরা পেলাম:
3. পরপর ২টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যিনি ২ দিয়ে বিভাজ্য বা নিঃশেষে বিভাজ্য।
আরো একটা ইন্টারেস্টিং ব্যপার হল:
4. শেষের অংকটিকে ২ দিয়ে ভাগ করার পর যে ভাগশেষ পাওয়া যায় পুরো সংখ্যা টাকেও ২ দিয়ে ভাগ করলে সেই একই ভাগশেষ পাওয়া যায়।
আরো কয়েকটা সংখ্যার বিভাজ্যতা দেখলে বিষয়গুলো আরো ক্লিয়ার হবে আশা করি।
৪, ৮, ১৬ দ্বারা বিভাজ্যতা:
২ দিয়ে বিভাজ্যতার সময় আমরা দেখেছি যে কোন সংখ্যা জোড় হলেই সে দুই দিয়ে নিঃশেষে বিভাজ্য অর্থাৎ কোন সংখ্যার শেষ ডিজিটটি ২ দিয়ে বিভাজ্য হলেই পুরো সংখ্যাটি ২ দিয়ে বিভাজ্য হয়। এখন ৪ এর ক্ষেত্রে দেখি কি হয়:
৮১২÷৪=২০৩, ৫০৮২৪÷৪=১২৭০৬ এগুলো ৪ দিয়ে নিঃশেষে বিভাজ্য, কিন্তু যদি ৮৬২ কে ৪ দিয়ে ভাগ করি তাহলে ২১৩ ভাগফল পাওয়ার পরেও ২ অবশিষ্ট থাকে একই ভাবে ৫০৮২৭ কে ৪ দিয়ে ভাগ করলে ১২৭০৬ ভাগফল পাওয়ার পরে ৩ অবশিষ্ট থাকে।
নিচের চিত্র দেখি:
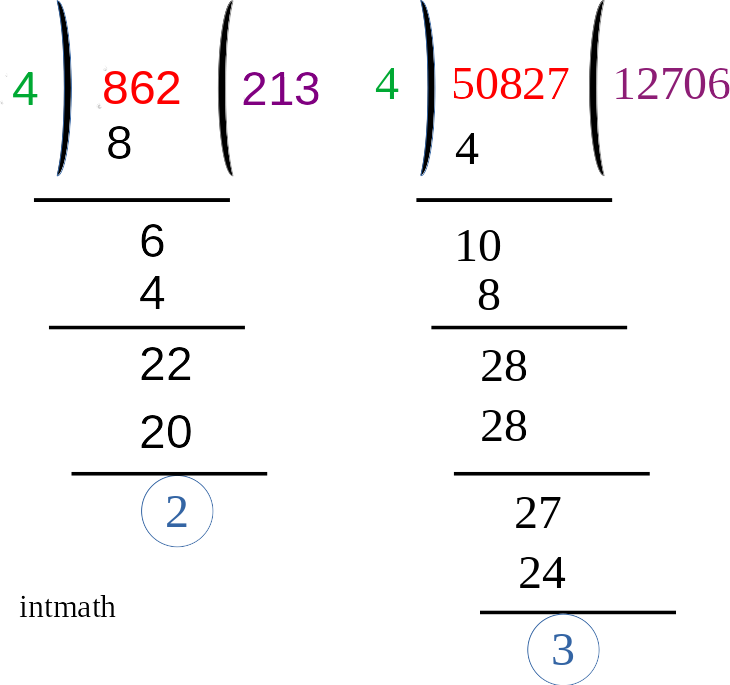
এখানে ব্যাপারটা কি ঘটতেছে: ৮১২ এর দিকে তাকালে আমরা দেখতে পাই এর শেষ দুইটা ডিজিট নিয়ে গঠিত সংখ্যা ১২, ৪ দিয়ে নিঃশেষে বিভাজ্য কিন্তু ৮৬২ এর বেলায় সেটা হচ্ছেনা কারন এর শেষ দুইটা ডিজিট নিয়ে গঠিত সংখ্যা ৬২, ৪ দিয়ে নিঃশেষে বিভাজ্য নয়, কারন তখন ২ অবশিষ্ট থাকে। একই ভাবে ৫০৮২৪ এর শেষ দুইটা ডিজিট নিয়ে গঠিত সংখ্যা ২৪ যা ৪ দিয়ে নিঃশেষে বিভাজ্য কিন্তু ৫০৮২৭ এর শেষ দুইটা ডিজিট নিয়ে গঠিত সংখ্যা ২৭, ৪ দিয়ে নিঃশেষে বিভাজ্য নয়, কারন তখন ৩ অবশিষ্ট থাকে। তারমানে এতক্ষণে আমরা বুঝে গেছি কোনো সংখ্যা যত বড়ই হোক তার শেষের দুইটা ডিজিট নিয়ে গঠিত সংখ্যা ৪ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ৪ দিয়ে নিঃশেষে বিভাজ্য হবে।
আচ্ছা আমরা জানি,
২১ = ২ যা ২ দিয়ে নিঃশেষে বিভাজ্য আবার
২২ = ৪ যা ৪ দিয়ে নিঃশেষে বিভাজ্য।
এখন আমরা একটু খেঁয়াল করলেই বুঝতে পারব যে কোনো সংখ্যার ক্ষেত্রে (সংখ্যাটি যত বড়ই হোক বা যত ছোটই হোক) যখন ২ এর পাওয়ার ১ তখন ঐ সংখ্যার শেষের ১টি অংক দিয়ে গঠিত সংখ্যা ২ দিয়ে বিভাজ্য হলেই সমগ্র সংখ্যাটি ২ দিয়ে বিভাজ্য হয়। আবার যখন ২ এর পাওয়ার ২ তখন ঐ সংখ্যার শেষের ২টি অংক দিয়ে গঠিত সংখ্যা ৪ দিয়ে বিভাজ্য হলেই সমগ্র সংখ্যাটি ৪ দিয়ে বিভাজ্য হয়।
এখন আমরা নিজেরাই একটা মজার জিনিস আবিষ্কার করে ফেলতে পারি!!
সেটা হলো…
:: আমি বলি আমি বলি..
:- হা শিওর, বলে ফেলো
:: সেটা হলো ২৩ = ৮ যা ৮ দিয়ে নিঃশেষে বিভাজ্য, এখানে ৮ বানানোর জন্য ২ এর পাওয়ার ৩ লাগতেছে, তারমানে কোনো সংখ্যার শেষের ৩টা ডিজিট দিয়ে গঠিত সংখ্যাটি ৮ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ৮ দিয়ে নিঃশেষে বিভাজ্য হবে?
:- হুম এক্স্যাক্টলি তাই 💕 তাহলে ১৬র বেলায় কি হবে বলে ফেলো
:: অউ খুবই ইজি.. ১৬র বেলায় হবে, ২৪ = ১৬ যা ১৬ দিয়ে নিঃশেষে বিভাজ্য, এখানে ১৬ বানানোর জন্য ২ এর পাওয়ার হিসেবে ৪ কে লাগতেছে, তারমানে কোনো সংখ্যার শেষের ৪টা ডিজিট দিয়ে গঠিত সংখ্যাটি ১৬ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ১৬ দিয়ে নিঃশেষে বিভাজ্য হবে।
:: আবারো ‘হুম এক্স্যাক্টলি তাই’
:- কিন্তু আমার একটা প্রশ্ন আছে, এই যে ২৩ = ৮, ২৪ = ১৬ এরা তো ৪ দিয়েও নিঃশেষে বিভাজ্য?
:: হুম এজন্যই তো যে সকল সংখ্যা ৮ বা ১৬ দিয়ে নিঃশেষে বিভাজ্য তারা সবাই ৪ দিয়েও নিঃশেষে বিভাজ্য।
:- বুঝছি।
:: তাহলে বলোতো যদি নিঃশেষে বিভাজ্য না হয় তাহলে কি হবে?
:- mmm.. কি দিয়ে নিঃশেষে বিভাজ্য না হয়?
:: ৪, ৮ বা ১৬ দিয়ে?
:- তাহলে ঐ সংখ্যাটিও ৪, ৮ বা ১৬ দিয়ে নিঃশেষে বিভাজ্য হবে না।
:: সো সুইট।
:- তাহলে নিঃশেষে বিভাজ্য না হলে কি হবে?
:: তখন নানান রকমের ভাগশেষ আসবে।
আচ্ছা ভাগশেষ গুলো কি কি আসবে তা দেখে নিই:
৪ এর সম্ভাব্য সকল ভাগশেষ গুলো হলো:
নিচের ছবি গুলো মনোযোগ দিয়ে দেখি:
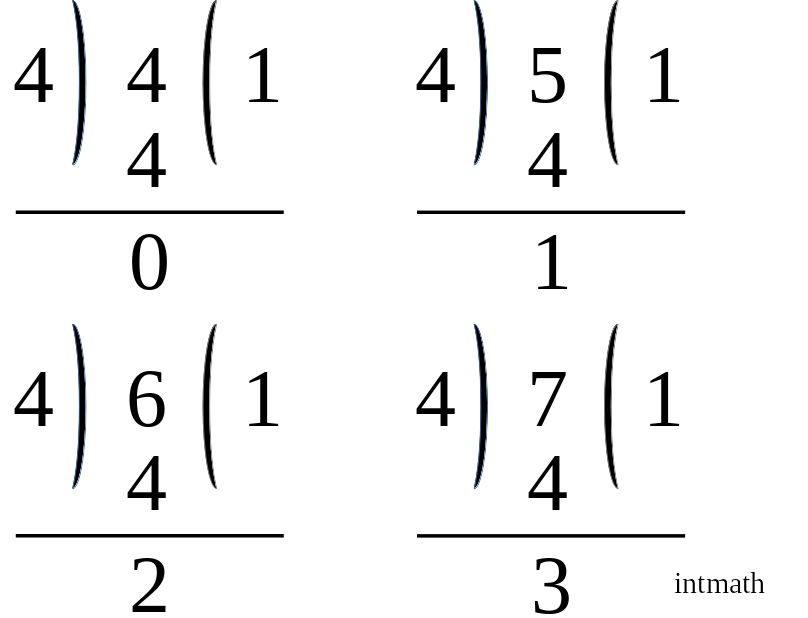
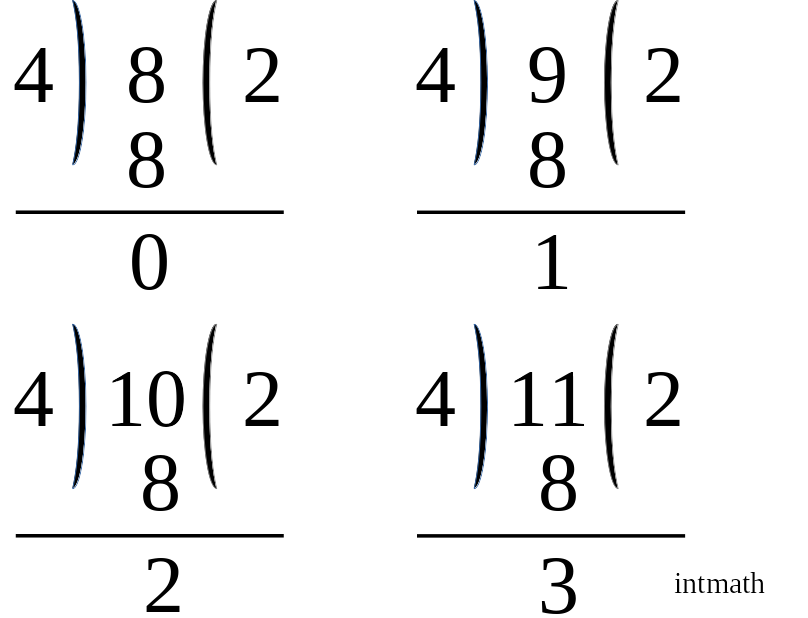
উপরের চিত্র থেকে আমরা দেখতে পাচ্ছি যে, ৪, ৫, ৬, ৭ কে ৪ দিয়ে ভাগ করলে যথাক্রমে ০, ১, ২ ও ৩ অবশিষ্ট থাকে বা ভাগশেষ থাকে। আবার নিচের চিত্র থেকে আমরা দেখতে পাচ্ছি যে, ৮, ৯, ১০, ১১ কে ৪ দিয়ে ভাগ করলে আাবারো যথাক্রমে ০, ১, ২ ও ৩ ই অবশিষ্ট থাকতেছে।
কারো কারো মনে প্রশ্ন আসতে পারে যে, ৪ দিয়ে বিভাজ্যতার সময় ভাগশেষ ৪ বা তার থেকে বড় হয়না কেন? হুম বড় হয়না কারন ৪ অবশিষ্ট থাকলে তো ৪ এর মধ্যে ৪ আরো একবার ভাগ যায়। আবার যদি অবশিষ্ট ৫ রাখতে চাই তাও হবেনা কারন ৫ এর মধ্যেও একটা আস্ত ৪ আছে (৪+১=৫) এই কারনে ভাগশেষ কখনই ভাজকের থেকে বড় হয় না।
তাহলে আমরা পেলাম:
1. কোনো সংখ্যা যত বড়ই হোক বা ছোটই হোক তার শেষের দুইটা ডিজিট নিয়ে গঠিত সংখ্যা ৪ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ৪ দিয়ে নিঃশেষে বিভাজ্য হবে।
2. যেকোনো সংখ্যাকে ৪ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০, ১, ২, ৩ এর যেকোনো ১টা হবে, এর বাইরে অন্য কিছু হওয়া সম্ভব না।
3. ৪ এর যেকোনো গুনিতক থেকে শুরু করে পরপর চারটি ক্রমিক সংখ্যাকে ৪ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে যেমন: উপরের চিত্র থেকে দেখতে পাচ্ছি যে ৪,৫,৬,৭ কে ৪ দিয়ে ভাগ করার পর আমরা যথাক্রমে ০,১,২,৩ ভাগশেষ পেয়েছি, আবার ৮,৯,১০,১১ বেলায়ও ০,১,২,৩ সেই একই ভাগশেষ রিপিট করতেছে। অর্থাৎ ৪ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ৪টি, ০ থেকে ৩ (৪-১) পর্যন্ত এবং কোনো একটি সংখ্যাকে ভাগ করলে এই ৪টির থেকে যেকোনো একটি ভাগশেষ আমরা পেয়ে থাকি।
4. পরপর ৪ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবেন যিনি ৪ দিয়ে বিভাজ্য বা নিঃশেষে বিভাজ্য।
5. শেষের অংক দুটি দ্বারা গঠিত সংখ্যাকে ৪ দিয়ে ভাগ করার পর যে ভাগশেষ পাওয়া যায়, পুরো সংখ্যা টাকেও ৪ দিয়ে ভাগ করলে সেই একই ভাগশেষ পাওয়া যায় (এই পইন্টটা একেবারেই কর্তৃপক্ষের ব্যক্তিগত মতামত, আপনারা পরীক্ষা-নিরীক্ষা, পর্যবেক্ষণ দ্বারা ভুল প্রমানিত করলে কর্তৃপক্ষকে জানানোর জন্য অনুরোধ জানানো থাকলো)
এখন তাহলে ৮ এর ঘটনা গুলো দেখি:
৮ এর সম্ভাব্য সকল ভাগশেষ গুলো হলো:
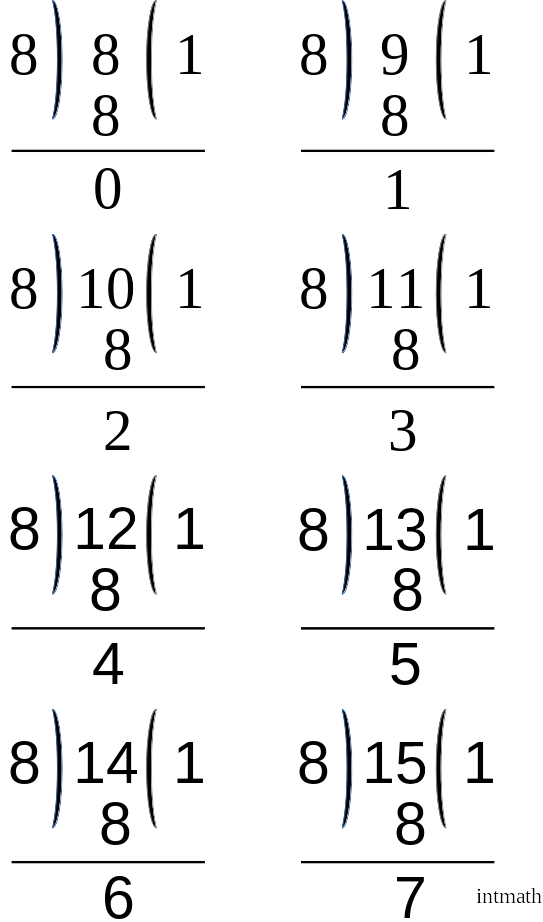
তাহলে উপরের চিত্র ও বর্ননা থেকে আমরা আবারো দেখতে পাচ্ছি যে:
1. কোনো সংখ্যার শেষের তিনটা ডিজিট নিয়ে গঠিত সংখ্যা ৮ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ৮ দিয়ে নিঃশেষে বিভাজ্য হবে।
2. যেকোনো সংখ্যাকে ৮ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০, ১, ২, ৩, ৪, ৫, ৬, ৭ এর মধ্যে যেকোনো ১টা হবে, এর বাইরে অন্য কিছু হওয়া সম্ভব না (ওই একই কারনে ভাগশেষ কখনই ভাজকের থেকে বড় হবে না।)
3. ৮ এর যেকোনো গুনিতক থেকে শুরু করে পরপর আটটি ক্রমিক সংখ্যাকে ৮ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে যেমন: উপরের চিত্র থেকে দেখতে পাচ্ছি যে ৮, ৯, ১০, ১১, ১২, ১৩, ১৪, ১৫ কে ৮ দিয়ে ভাগ করার পর আমরা যথাক্রমে ০,১,২,৩,৪,৫,৬,৭ কে ভাগশেষ হিসেবে পেয়েছি। অর্থাৎ ৮ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ৮টি, ০ থেকে ৭ (৮-১) পর্যন্ত এবং কোনো একটি সংখ্যাকে ভাগ করলে এই ৮ টির থেকে যেকোনো একটি ভাগশেষ আমরা পেয়ে থাকি।
4. পরপর ৮টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে ৮ দিয়ে নিঃশেষে বিভাজ্য।
5. শেষের অংক তিনটি দ্বারা গঠিত সংখ্যাকে ৮ দিয়ে ভাগ করার পর যে ভাগশেষ পাওয়া যায়, পুরো সংখ্যা টাকেও ৮ দিয়ে ভাগ করলে সেই একই ভাগশেষ পাওয়া যায় (ঐ যে… কর্তৃপক্ষকে জানানোর জন্য অনুরোধ জানানো থাকলো)
তাহলে একই ভাবে আমরা ১৬র বিভাজ্যতা সম্পর্কেও বলতে পারি যে:
1. কোনো সংখ্যা যত বড়ই হোক বা ছোটই হোক তার শেষের চারটা ডিজিট নিয়ে গঠিত সংখ্যা ১৬ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ১৬ দিয়ে নিঃশেষে বিভাজ্য হবে।
2. কোনো সংখ্যাকে ১৬ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০ থেকে ১৫ পর্যন্ত এর যেকোনো ১টা সংখ্যা হতে পারে, এর বাইরে অন্য কিছু হবে না। অর্থাৎ ১৬ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ১৬টি, ০ থেকে ১৫ (১৬-১) পর্যন্ত এবং কোনো একটি সংখ্যাকে ভাগ করলে এই ১৬ টির থেকে যেকোনো একটি ভাগশেষ আমরা পেয়ে থাকি।
3. ১৬ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ১৬টি ক্রমিক সংখ্যাকে ১৬ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে। এর সত্যতা প্রমানের ব্যপারটি ম্যাথমেটিশিয়ানদের ঘাড়ে চাপিয়ে দেওয়া হল।
4. পরপর ১৬ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যেটা কিনা ১৬ দিয়ে নিঃশেষে বিভাজ্য।
5. শেষের ৪টি অংক দ্বারা গঠিত সংখ্যাকে ১৬ দিয়ে ভাগ করার পর যে ভাগশেষ পাওয়া যায়, পুরো সংখ্যা টাকেও ১৬ দিয়ে ভাগ করলে সেই একই ভাগশেষ পাওয়া যায়।
এখন তাহলে ঠিক একই ভাবে আমরা ৩২, ৬৪, … ইত্যাদির বিভাজ্যতার ঘটনা গুলোও নির্ণয় করতে পারবো।
পুনশ্চ-১: এই পোষ্ট লেখার সময় আমার মমতাময়ী মাকে বারবার অনুভব করেছি কারন একেবারে পিচ্চিকালে গুণ-ভাগ শেখার সময় যখন ভাজ্য/ ভাজক গুলিয়ে ফেলতাম তখন ‘যে ভাজে সে হলো ভাজক’, ‘যাকে ভাজা হয় সে হলো ভাজ্য’ এই টার্ম গুলো আমার “মাই ডিয়ার মম” এর কাছ থেকেই শিখেছি।
পুনশ্চ-২: ইনশাল্লাহ খুব শীঘ্রই আসছে বিভাজ্যতার ২য় পর্ব।


ওয়াও! অনেক কিছু শিখলাম! ধন্যবাদ! 😊
আপনাকেও ধন্যবাদ 😊 কিছু শিখতে পারলেই আমার সার্থকতা