বিভাজ্যতা পর্ব-৩

বিভাজ্যতা পর্ব-১ আর বিভাজ্যতা পর্ব-২ খুব মনোযোগ দিয়ে পড়ে থাকলে আমরা বিভাজ্যতার অনেক ট্রিকই ইতোমধ্যে বুঝে গিয়েছি। এখানে আমরা ৫, ৬, ১০, ১২, ১৪ ও ১৫ এর বিভাজ্যতা নিয়ে আলোচনা করব। কথা না বাড়িয়ে মুল আলোচনায় চলে যাই।

প্রথমে আমরা ৬ এর বিভাজ্যতা দেখি কারন এখানে একটু বেশি মনোসংযোগ করতে হবে।
৬ এর বিভাজ্যতা:

সবার আগে আমরা ৬ এর ঘরের নামতা টা একটু দেখে তাহলে বাকি সবকিছু বুঝতে সুবিধা হবে।
৬ × ১ = ৬
৬ × ২ = ১২
৬ × ৩ = ১৮
৬ × ৪ = ২৪
৬ × ৫ = ৩০
৬ × ৬ = ৩৬
৬ × ৭ = ৪২ ইত্যাদি

তাহলে আমরা দেখতে পাচ্ছি যে গুনিতক গুলো সবাই জোড় সংখ্যা। এখানে বলে রাখা ভাল যে, কোনো জোড় সংখ্যার গুণিতক অবশ্যই আরেকটি জোড় সংখ্যা হবে। কেন হয় সেটাও আমরা সহজেই বুঝতে পারব।
খুব অল্প কথায় বলি:
গুণ তো আসলে যোগেরই রিপিটেশন বা পুনরাবৃত্তি। যেমন, ৬ × ৩ = ১৮ এখানে আসলে ৬ কে ৩ বার যোগ করা হয় (৬+৬+৬=১৮) তারমানে আসলে বারবার যোগের ধারণা থেকেই গুণের ধারনা এসেছে। তো যেকোনো জোড় সংখ্যাকে যতবারই যোগ করা হোক তার যোগফল সবসময়ই জোড় সংখ্যা হবে। এজন্য যেকোনো জোড় সংখ্যার গুণিতক আরেকটি জোড় সংখ্যা হয়।
এখন আমরা আবার মূল আলোচনায় ফিরে যাই।
তাহলে ৬ এর সকল গুনিতক হলো জোড় সংখ্যা। আবার ৩ এর বিভাজ্যতা থেকে আমরা জানি যে, কোনো সংখ্যার অংকগুলোর সমষ্টি ৩ দিয়ে বিভাজ্য হলে ঐ সংখ্যাটি ৩ দিয়ে বিভাজ্য হয়। তাহলে নামতার দিকে তাকালে আমরা দেখতে পাচ্ছি,
৬ × ২ = ১২ এখানে ১+২=৩ যা ৩ দিয়ে নিঃশেষে বিভাজ্য
৬ × ৩ = ১৮ এখানে ১+৮=৯ যা ৩ দিয়ে নিঃশেষে বিভাজ্য
৬ × ৪ = ২৪ এখানে ২+৪=৬ যা ৩ দিয়ে নিঃশেষে বিভাজ্য
তাহলে আমরা দেখতে পাচ্ছি যে ৬ এর গুনিতক সবাই জোড় সংখ্যা এবং একই সাথে ৩ দিয়ে বিভাজ্য! তাহলে আমরা এই সিদ্ধান্তে উপনীত হতে পারি যে, কোনো সংখ্যা একই সাথে ২ এবং ৩ দিয়ে বিভাজ্য হলে ঐ সংখ্যাটি ৬ দিয়ে বিভাজ্য হবে। অন্য ভাবে বলা যায় কোনো জোড় সংখ্যা ৩ দিয়ে বিভাজ্য হলে সে ৬ দিয়েও বিভাজ্য হবে।

আচ্ছা খুব তো বুঝলাম এখন দেখি ৬ এর অবিভাজ্যতা বা কোনো সংখ্যা ৬ দিয়ে নিঃশেষে বিভাজ্য না হলে কি কি ভাগশেষ আসতে পারে:

আগের পর্ব গুলো থেকে আমরা সবাই সুন্দর মতো বুঝে গিয়েছি যে, কোনো সংখ্যার ভাগশেষ ০ থেকে শুরু করে ঐ সংখ্যার আগ পর্যন্ত (n-১) যেকোনো সংখ্যাই হতে পারে কিন্তু ঐ সংখ্যার বা তার থেকে বড় কোনো সংখ্যা হবেনা কারন ওইযে ভাগশেষ কখনো ভাজকের থেকে বড় হয়না। তো এখানেও ৬ এর জন্য সম্ভাব্য ভাগশেষ হবে ৬ টি, ০ থেকে ৫ পর্যন্ত।

তাহলে আমরা পেলাম:

১। কোনো জোড় সংখ্যা ৩ দিয়ে নিঃশেষে বিভাজ্য হলে ঐ সংখ্যাটি ৬ দিয়ে নিঃশেষে বিভাজ্য হবে।
২। কোনো সংখ্যাকে ৬ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০, ১, ২, ৩, ৪ ও ৫ এর মধ্যে যেকোনো ১টা হবে, এর বাইরে অন্য কিছু হবে না (কেন হবেনা তা পর্ব-১ থেকে দেখেছি)
৩। ৬ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ৬টি ক্রমিক স্বাভাবিক সংখ্যাকে ৬ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে এবং সেগুলো হবে ০ থেকে ৫ পর্যন্ত। অর্থাৎ ৬ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ৬টি।
৪। পরপর ৬ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে কিনা ৬ দিয়ে নিঃশেষে বিভাজ্য।

৫ এর বিভাজ্যতা:

৫ দিয়ে বিভাজ্যতার ব্যপারটা হয়ত আমরা অনেকেই ছোট বেলায় নামতা শেখার সময়ই খেয়াল করেছি। এটা খুবই সহজ ব্যাপার। আচ্ছা, আগে ৫ এর ঘরের নামতা টা আরেকবার দেখে নিই:

৫ × ১ = ৫
৫ × ২ = ১০
৫ × ৩ = ১৫
৫ × ৪ = ২০
৫ × ৫ = ২৫
৫ × ৬ = ৩০
৫ × ৭ = ৩৫
৫ × ৮ = ৪০
৫ × ৯= ৪৫

এখানে আমরা একটু খেঁয়াল করলেই দেখতে পাই যে, ৫ এর গুনিতকের সবার একক স্থানীয় অংকটি ০ অথবা ৫। এখানে বলে রাখা ভালো যে গুনিতক আর গুনফল একই জিনিস। যেমন, ৫ × ৩ = ১৫ এখানে ৩ আর ৫ এর গুনফল ১৫ হলো ৫ এরও গুনিতক একই সাথে ৩ এরও গুনিতক।
নিচের ছবিটি দেখি:

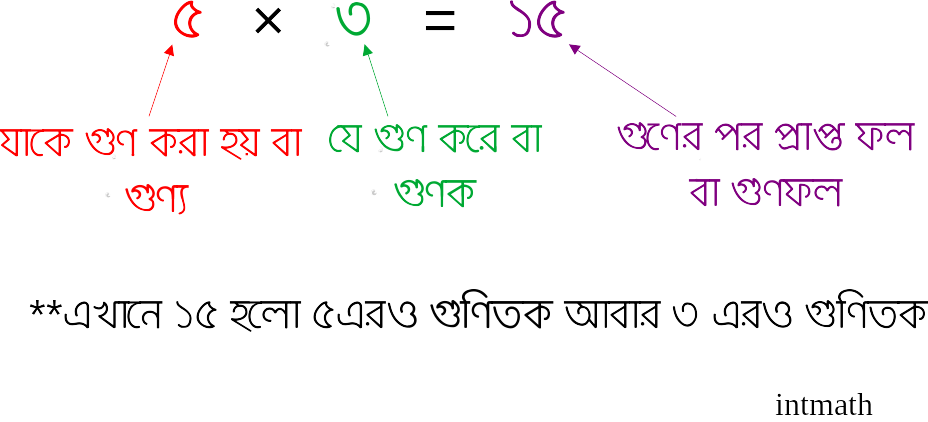
তাহলে উপরের নামতা থেকে আমরা দেখতে পাচ্ছি যে, ৫ এর গুনিতকের সবার একক স্থানীয় অংকটি ০ অথবা ৫। তারমানে কোনো সংখ্যাকে ৫ দিয়ে নিঃশেষে বিভাজ্য হতে হলে সেই সংখ্যার শেষের অংকটিকে ০ অথবা ৫ হতে হবে। যেমন, ১০৩৭৪৫, ৯১০৩৭০ ইত্যাদি।
আচ্ছা আগের পর্ব গুলো আমরা মনোযোগ দিয়ে পড়ে থাকলে সহজেই বুঝবো যে, কোনো সংখ্যার শেষ অংকটি ০ বা ৫ কোনোটিই না হলে ওই সংখ্যাটি ৫ দিয়ে নিঃশেষে বিভাজ্য হবেনা। আর নিঃশেষে বিভাজ্য না হলে সম্ভাব্য ভাগশেষ গুলো কি কি হতে পারে তাও আমরা শিখে গিয়েছি। এখন ৫ এর সম্ভাব্য ভাগশেষ গুলো নিচের ছবিতে দেখি:

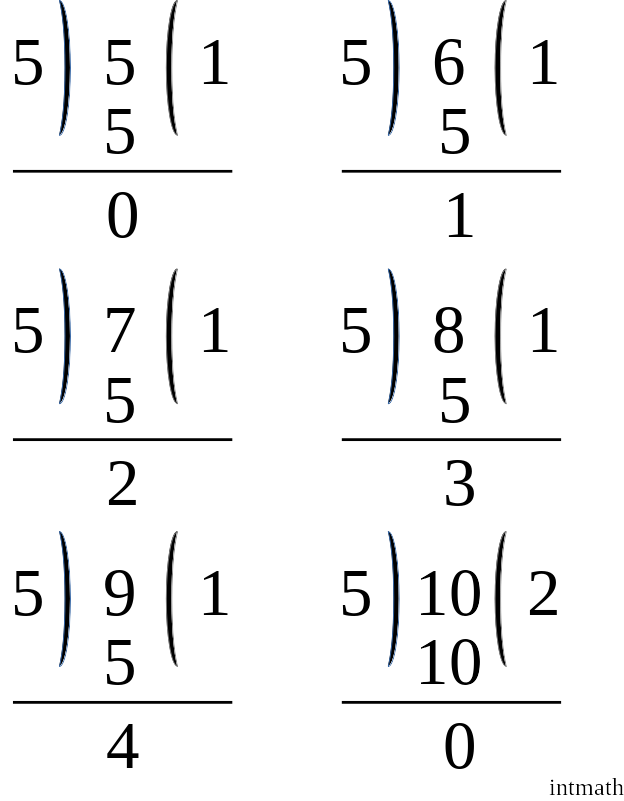
তাহলে আগের মতই আমরা পেলাম:

১। কোনো সংখ্যার শেষের অংকটি (একক স্থানীয় অংকটি) ০ অথবা ৫ হলে পুরো সংখ্যাটিই ৫ দিয়ে নিঃশেষে বিভাজ্য হবে। অথবা শেষের ২ টা ডিজিট নিয়ে গঠিত সংখ্যা ৫ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ৫ দিয়ে নিঃশেষে বিভাজ্য হবে।
২। কোনো সংখ্যাকে ৫ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০, ১, ২, ৩ ও ৪ এর মধ্যে যেকোনো ১টা হবে, এর বাইরে অন্য কিছু হবে না (কেন হবেনা তা পর্ব-১ থেকে দেখেছি)
৩। ৫ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ৫টি ক্রমিক স্বাভাবিক সংখ্যাকে ৫ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে যেমন: উপরের চিত্র থেকে দেখতে পাচ্ছি যে ৫, ৬, ৭, ৮, ৯ কে ৫ দিয়ে ভাগ করলে যথাক্রমে ০, ১, ২,৩ ও ৪ ভাগশেষ থাকে। অর্থাৎ ৫ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ৫টি, ০ থেকে ৫-১=৪ পর্যন্ত এবং কোনো একটি সংখ্যাকে ভাগ করলে এই ৫টির থেকে যেকোনো একটি ভাগশেষ পাওয়া যায়।
৪। পরপর ৫ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে কিনা ৫ দিয়ে নিঃশেষে বিভাজ্য।
৫। শেষের অংক দুটি দ্বারা গঠিত সংখ্যাকে ৫ দিয়ে ভাগ করার পর যে ভাগশেষ পাওয়া যায়, পুরো সংখ্যা টাকেও ৫ দিয়ে ভাগ করলে সেই একই ভাগশেষ পাওয়া যায়।

১০ এর বিভাজ্যতা:

স্বরণ কালের ইতিহাসে সবচেয়ে সহজ বিষয় হলো ১০ এর বিভাজ্যতা নির্ণয়। কোনো সংখ্যার এককের ঘরে ০ থাকলেই বোঝা যায় যে সে ১০ দিয়ে নিঃশেষে বিভাজ্য অন্যথায় ১০ দিয়ে নিঃশেষে বিভাজ্য হবেনা।

অলরেডি আমরা বিভাজ্যতা, সম্ভাব্য সকল ভাগশেষ ইত্যাদি নির্নয় শিখে গিয়েছি এখানে তাই আর সেসব আলোচনার পুনরাবৃত্তি করা হলোনা।
তাহলে এখন আমরা জানি যে:

১। কোনো সংখ্যার শেষের অংকটি (একক স্থানীয় অংকটি) ০ হলেই পুরো সংখ্যাটিই ১০ দিয়ে নিঃশেষে বিভাজ্য হবে। অথবা শেষের ২ টা ডিজিট নিয়ে গঠিত সংখ্যা ১০ দিয়ে নিঃশেষে বিভাজ্য হলে পুরো সংখ্যাটিই ১০ দিয়ে নিঃশেষে বিভাজ্য হবে।
২। কোনো সংখ্যাকে ১০ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ হবে ০ থেকে ৯ পর্যন্ত যেকোনো ১টা সংখ্যা, এর বাইরে অন্য কিছু হবে না (কেন হবেনা তা পর্ব-১ থেকে দেখেছি)
৩। ১০ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ১০টি ক্রমিক স্বাভাবিক সংখ্যাকে ১০ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে এবং সেগুলো হবে ০ থেকে ৯ পর্যন্ত। অর্থাৎ ১০ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ১০টি।
৪। পরপর ১০ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে ১০ দিয়ে নিঃশেষে বিভাজ্য।
৫। শেষের অংক দুটি দ্বারা গঠিত সংখ্যাকে ১০ দিয়ে ভাগ করার পর যে ভাগশেষ পাওয়া যায়, পুরো সংখ্যা টাকেও ১০ দিয়ে ভাগ করলে সেই একই ভাগশেষ পাওয়া যায়।

ইতোমধ্যে আমরা বিভাজ্যতার বৈশিষ্ট, আচার-আচরণ শিখে গেছি এখন ১২,১৪ আর ১৫ এর বিভাজ্যতা সম্পর্কে খুব সংক্ষেপে আলোচনা করব: এদের সবার বিভাজ্যতাই এখানে ৬ এর বিভাজ্যতার মত করে হাল্কাভাবে ব্যাক্ষা করা হলো:

১২ এর এর বিভাজ্যতা:

১। কোনো সংখ্যা ৩ এবং একই সাথে ৪ দিয়ে নিঃশেষে বিভাজ্য হলে ঐ সংখ্যাটি ১২ দিয়ে নিঃশেষে বিভাজ্য হবে।
২। কোনো সংখ্যাকে ১২ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০ থেকে ১১ পর্যন্ত এর মধ্যে যেকোনো ১টা সংখ্যা হবে, এর বাইরে অন্য কিছু হবে না (কেন হবেনা তা পর্ব-১ থেকে দেখেছি)
৩। ১২ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ১২টি ক্রমিক স্বাভাবিক সংখ্যাকে ১২ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে এবং সেগুলো হবে ০ থেকে ১১ পর্যন্ত। অর্থাৎ ১২ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ১২টি।
৪। পরপর ১২ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে কিনা ১২ দিয়ে নিঃশেষে বিভাজ্য।

১৪ এর এর বিভাজ্যতা:

১। কোনো সংখ্যা ২ দিয়ে এবং একই সাথে ৭ দিয়ে নিঃশেষে বিভাজ্য হলে অর্থাৎ কোনো জোড় সংখ্যা ৭ দিয়ে নিঃশেষে বিভাজ্য হলে ঐ সংখ্যাটি ১৪ দিয়ে নিঃশেষে বিভাজ্য হবে। (৭ এর বিভাজ্যতা আগামী পর্বে দেখানো হবে ইনশাল্লাহ)
২। কোনো সংখ্যাকে ১৪ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০ থেকে ১৩ পর্যন্ত এর মধ্যে যেকোনো ১টা সংখ্যা হবে, এর বাইরে অন্য কিছু হবে না (কেন হবেনা তা পর্ব-১ থেকে দেখেছি)
৩। ১৪ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ১৪টি ক্রমিক স্বাভাবিক সংখ্যাকে ১৪ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে এবং সেগুলো হবে ০ থেকে ১৩ পর্যন্ত। অর্থাৎ ১৪ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ১৪টি।
৪। পরপর ১৪ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে কিনা ১৪ দিয়ে নিঃশেষে বিভাজ্য।

১৫ এর এর বিভাজ্যতা:

১। কোনো সংখ্যা ৩ এবং একই সাথে ৫ দিয়ে নিঃশেষে বিভাজ্য হলে ঐ সংখ্যাটি ১৫ দিয়ে নিঃশেষে বিভাজ্য হবে।
২। কোনো সংখ্যাকে ১৫ দিয়ে ভাগ করলে সম্ভাব্য ভাগশেষ ০ থেকে ১৪ পর্যন্ত এর মধ্যে যেকোনো ১টা সংখ্যা হবে, এর বাইরে অন্য কিছু হবে না (কেন হবেনা তা পর্ব-১ থেকে দেখেছি)
৩। ১৫ এর যেকোনো গুনিতক থেকে শুরু করে পরপর ১৫টি ক্রমিক স্বাভাবিক সংখ্যাকে ১৫ দিয়ে ভাগ করলে ভাগশেষ গুলোও ক্রমিক হবে এবং সেগুলো হবে ০ থেকে ১৪ পর্যন্ত। অর্থাৎ ১৫ দিয়ে বিভাজ্যতার সময় সম্ভাব্য ভাগশেষ হলো ১৫টি।
৪। পরপর ১৫ টি ক্রমিক সংখ্যার মধ্যে একটা এবং কেবল মাত্র একটা সংখ্যা অবশ্যই থাকবে যে কিনা ১৫ দিয়ে নিঃশেষে বিভাজ্য।

শেষের ৩টার ব্যাক্ষা ফাকিবাজি করে দেখানো হলো। আগের বিভাজ্যতা গুলো ভালো মতো শিখলে এই তিনটাও নিজেরা বিশ্লেষণ করতে পারবে।
আজ তাহলে এপর্যন্তই থাক।