Numbers

এই পোস্টে Number বা সংখ্যা এবং তার শ্রেণীবিভাগ নিয়ে সংক্ষিপ্ত আলোচনা হবে:

Number এর বাংলা প্রতিশব্দ হল সংখ্যা আর সংখ্যা হল সেই জিনিস যাদেরকে আমরা কোনোকিছু গননা বা পরিমাপের সময় ব্যবহার করি। তো সংখ্যা জানার আগে আমাদের অংক কি সেটা ভালমত জানতে হবে। অংক হল গনিতের কিছু সাংখ্যিক প্রতীক যার দ্বারা আমরা সংখ্যাকে প্রকাশ করি। আচ্ছা ব্যাপারটা আরো ক্লিয়ার করা যাক:

আমরা তো সবাই ইংরেজি বর্ণমালা, বাংলা বর্ণমালা চিনি যেমন: a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, … … … ইত্যাদি। এখান থেকে আমরা ইচ্ছামত বর্ণ নিয়ে শব্দ সাজাতে পারি। যেমন, উপরের বর্ণগুলো থেকে a, h, m, t বর্ণ চারটি নিয়ে আমরা math শব্দটি গড়তে পারি। আবার কারো নাম “অমুক” হলে o, m, u, k এই চারটি বর্ণ নিযে তার নাম লিখতে পারি omuk আবার নিচের ছবির মত কোনোকিছু থামাতে চাইলে আমরা stop শব্দটি ব্যবহার করি, এটাও তো s, t, o, p বর্ণ চারটি নিয়ে গঠিত।

এভাবে আমরা ইচ্ছামত বর্ণ নিয়ে ইচ্ছামত শব্দ গড়তে পারি। গনিতেও অংক আর সংখ্যা ঠিক এভাবেই কাজ করে। বর্ণ গুলোকে অংক বা digit হিসেবে চিন্তা করলেই বুঝতে পারব যে এক বা একাধিক বর্ণ নিয়ে যেমন শব্দ গঠিত হয় তেমনি একাধিক অংক নিয়ে সংখ্যা গঠিত হয়। যেমন, ১, ২, ৩ এই তিনটি অংক নিয়ে ১২৩ সংখ্যাটি গঠিত হয় আবার ৫ ও ৬ নিয়ে ৫৬ (ছাপ্পান্ন) সংখ্যাটি গঠিত হয়। আবার ১, ২, ৩ এই তিনটি অংক নিয়ে শুধু ১২৩ই গঠিত হয় না বরং ১৩২, ২১৩, ৩১২, ২৩১, ৩২১ ইত্যাদিও হয়। নিচের ছবিটি দেখলে আরো ভালমত বোঝা যাবে:

এখানে o, p, s, t অক্ষর গুলো মিলে বিভিন্ন রকমের শব্দ গঠন করেছে একই ভাবে ১, ২, ৩, ৪ অংক গুলো মিলে বিভিন্ন রকমের সংখ্যা গঠন করেছে।
তবে সংখ্যা গঠনের সময় একটা ব্যাপার মেনে চলতে হয়, ব্যাপারটা হল অংকপাতন। বলি সে আবার কি! গনিতে সংখ্যা গঠনের সময় অংকগুলোকে তাদের স্থানীয় মান হিসাব করে বসানো হয় (আমরা তো সবাই জানি সংখ্যার বাম দিক থেকে একক, দশক, শতক এভাবে গননা করতে হয়) তো এভাবে স্থানীয় মান হিসাব করে অংক বসিয়ে সংখ্যা বানানোর নিয়মকে অংকপাতন বলে।
আচ্ছাহ তা তো খুব বুঝলাম কিন্তু শুধু একটা ৫ বা একটা ২ কি সংখ্যা হতে পারবে? হুম পারবে। a যেমন একটা অক্ষর আবার a যখন নিজেই একটা অর্থ প্রকাশ করে (a = একটি) যেমন, it is a pen, that is a cow তখন a নিজেই একটা শব্দ ওরকম যদি বলি ৫টা কলম, ২টা বই তখন ৫, ২ এগুলো সংখ্যা হিসেবে কাজ করবে।

তাহলে এখন আমরা জানি আমাদের কতগুলো অংক আছে, ১০টি, শূন্য থেকে ৯ পর্যন্ত (০,১,২,….৮,৯) কিন্তু সংখ্যা আছে অসীম! আসলেই!!!? হু, এই ১০টা অংক ব্যবহার করে আমরা কোটি কোটি অর্থাৎ এক কোটি, ২ কোটি, ১০০ কোটি, ২০০ কোটি এভাবে হাজার হাজার কোটি পর্যন্ত সংখ্যা লিখতে পারি। আসলে ১০ ভিত্তিক সংখ্যা পদ্ধতি আমাদের দুই হাতের ১০ টা আঙ্গুল ব্যবহার করে গননার ধারনা থেকে এসেছে। সংখ্যার আবিষ্কার ও এর ব্যবহার নিয়ে নানা মতভেদ রয়েছে এবং এতো বড় আর অসীম ধারনা যে কোনো একজন ব্যক্তি বা একটি মাত্র জেনারেশনের মাধ্যমে সৃষ্টি হওয়া সম্ভব নয় তা সহজেই বোঝা যায়। এখন দেখব আমরা যে এই সমস্ত সংখ্যাকে ব্যাবহার করি তাদেরকে কতগুলো ক্যাটাগরি বা ভাগের মধ্যে ফেলা যায়।

সংখ্যার শ্রেনীবিভাগ:

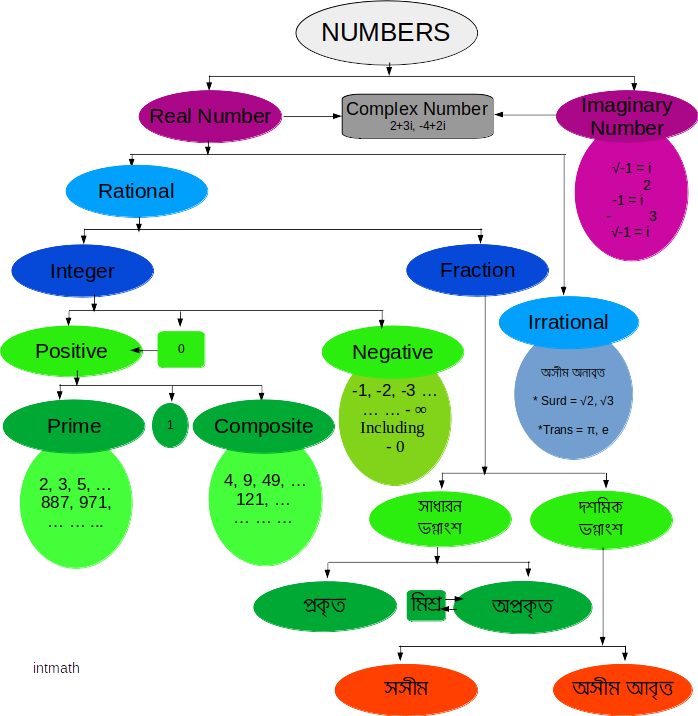
উপরের ছকে দেখতে পাচ্ছি সংখ্যা ২ প্রকার মতান্তরে ৩প্রকার:
A. বাস্তব সংখ্যা বা Real Number (ℝ)
B. কাল্পনিক সংখ্যা বা imaginary number (i)
মতান্তরের ব্যাপারটা হল complex number বা জটিল সংখ্যাকে আরেকটা প্রকারভেদ দেওয়া কিন্তু বাস্তব আর কাল্পনিক সংখ্যা মিলিয়েই তো আমরা জটিল সংখ্যা পাই। যেমন, 2+3i, 3-5i, 0+9i অর্থাৎ জটিল সংখ্যার দুইটা পার্ট থাকে একটা real part অন্যটা imaginary part এখানে real part বা imaginary part যেকোনোটা শুন্য হতে পারে।
** imaginary ও complex number নিয়ে পরে কোনো পোষ্টে আলোচনা হবে ইনশাল্লাহ।

নিচের ছবিটি দেখলে আরো ভালো মত বোঝা যাবে।

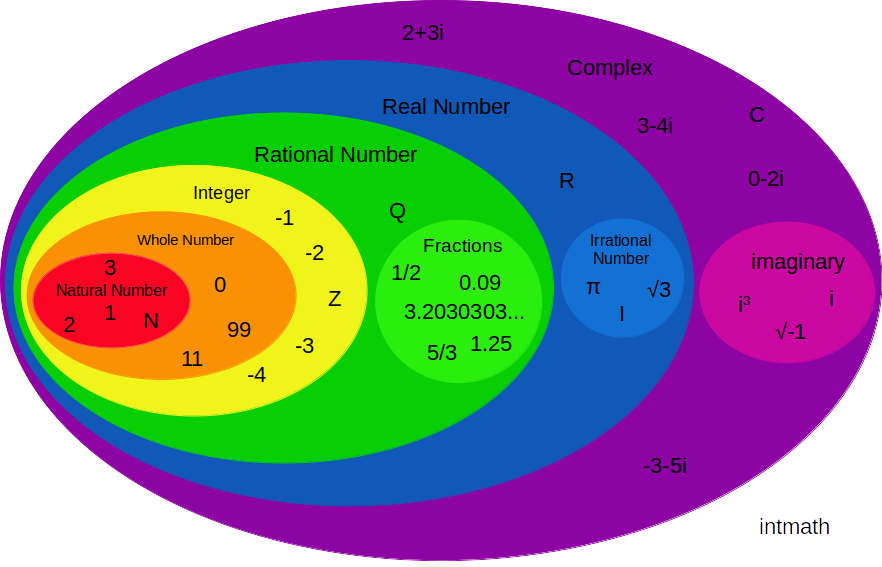
A.বাস্তব সংখ্যা বা Real Number: আসলে সংখ্যা বলতে আমরা যাদেরকে চিনি বা বাস্তব জীবনে বিভিন্ন হিসাব নিকাশ ও গননার ক্ষেত্রে যেসব সংখ্যা ব্যবহার করে থাকি তারাই বাস্তব সংখ্যা। অন্য কথায় যে সব সংখ্যাকে সংখ্যারেখার উপর চিহ্নিত করা যায় বা জায়গা দেয়া যায় তাদেরকে বাস্তব সংখ্যা বলে। ( সংখ্যারেখা হল শুধু মাত্র x অক্ষ বরাবর যে একমাত্রিক রেখা সেটা )
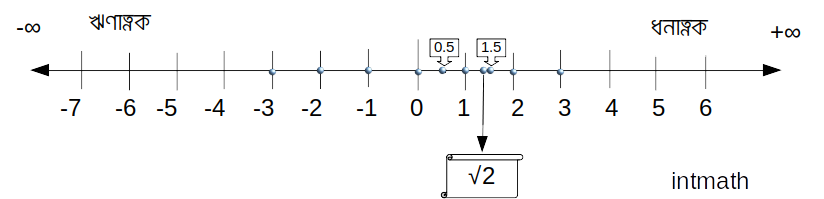
যেমন নিচের সংখ্যারেখাটি সকল বাস্তব সংখ্যার নির্দেশক:

উপরের চিত্র থেকে আমরা দেখতেই পাচ্ছি যে কাল্পনিক আর জটিল সংখ্যা বাদে ধনাত্নক, ঋণাত্নক, পূর্ণ, ভগ্নাংশ, মূলদ, অমূলদ সকল সংখ্যাই বাস্তবসংখ্যার অন্তর্গত।

বাস্তবসংখ্যাকে ২ ভাগে ভাগ করা হয়:
1. Rational বা মূলদ সংখ্যা ( ℚ )
2. Irrational বা অমূলদ সংখ্যা (I)

1.Rational বা মূলদ সংখ্যা ( ℚ ): Rational হয়েছে Ratio থেকে। Ratio অর্থ অনুপাত, প্রশ্ন হল কিসের অনুপাত? উত্তর হল দুইটা পূর্ণসংখ্যার অনুপাত। তাহলে হলে Rational হল যাকে অনুপাত আকারে প্রকাশ করা যায়। আরো সূক্ষ ভাবে বললে হয় যে সকল সংখ্যাকে দুইটি পূর্ণসংখ্যার অনুপাত আকারে প্রকাশ করা যায় তাদেরকে Rational Number বা মূলদ সংখ্যা বলে। যেমন, ১ = \frac ১ ১ বা \frac {-২} {-২} বা \frac {১০} {১০} আবার ২ = \frac ২ ১ বা \frac {১৪} { ৭} বা \frac {১৬} { ৮} ইত্যাদি।

অন্য ভাবে বলা যায় দুইটি পূর্ণসংখ্যার Quotient বা ভাগফলই হল মূলদ সংখ্যা। এই Quotient এসেছে Italian শব্দ quoziente থেকে যার অর্থ ভাগফল। আর Quotient এর শুরুর অক্ষর Q তাই সকল মূলদ সংখ্যার সেটকে ℚ দিয়ে প্রকাশ করা হয়।

বলি দুইটা Q দুই রকম ক্যান, আসলে Q কে স্পেশালিটি দেওয়া হয়েছে তাই ও ℚ হয়ে গেছে! একটু খেয়াল করলে দেখা যায় যে ℝ, ℚ, ℤ সব special symbol গুলো এরকম। আসলে এগুলো দিয়ে কিছু বিশেষ বিশেষ সংখ্যার সেটকে বোঝানো হয় তাই এদেরকে বিশেষ গুরুত্ব দিয়ে লেখা হয় জন্য ওরকম double struck capital form এ লেখা হয়।

নিচের ঘটনাগুলো মনোযোগ নিয়ে দেখি:

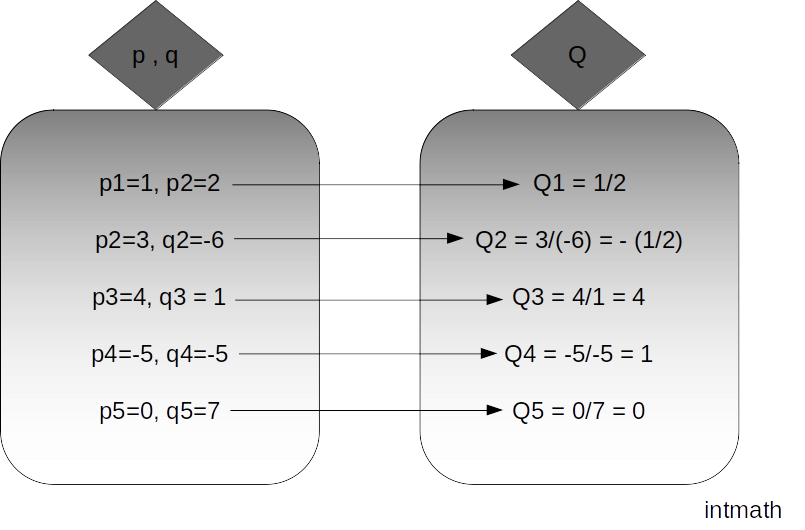
এখন তাহলে এগুলোও বুঝবো:
মনে করি, p একটি পূর্ণসংখ্যা; অর্থাৎ p = ১,২,৩,৪, … … … ইত্যাদি
এবং q আরেকটি পূর্ণসংখ্যা অর্থাৎ q = ১,২,৩,৪, … … … ইত্যাদি
এদের দুইজনের অনুপাত করলে হবে p:q বা \frac p q;
p = ১, q = ২ নিলে \frac p q = \frac ১ ২;
আবার p = ২, q = ৫ নিলে \frac p q = \frac ২ ৫;
আবার p = ৩, q = ১ নিলে \frac p q = \frac ৩ ১ = ৩; তারমানে সকল পূর্ণসংখ্যাও মূলদ সংখ্যা (২,৩,৪,৫, এভাবে সকল পূর্ণসংখ্যার নিচে তো মনে মনে ১ থাকে)

এখানে কয়েকটা খেয়ালযোগ্য ব্যাপার আছে,

১। p আর q এর মান সমান হলে তো ফলাফল সবসময়ই ১ হবে যেমন, \frac ২ ২ = ১; \frac ৩ ৩ = ১; \frac ৯ ৯=১;

২। p এর মান শুন্য হলে তো ফলাফল সবসময়ই ০ হবে যেমন, \frac ০ ২ = ০; \frac ০ ৩ = ০; \frac ০ ৯=০;
ঘটনাটা হালকা ভাবে ব্যাক্ষা করা হল:
মনে করি আমার কাছে এরোপ্লেন আছে ৬টা এগুলো আমার ৩জন প্রানের বন্ধুকে ভাগ করে দিব (মুক্তহস্তে দান আর কি) তাহলে প্রত্যেকে \frac ৬ ৩ = ২ টা করে এরোপ্লেন পাবে। কিন্তু আমার বন্ধু যদি তিনজনই থাকে আর আমার কাছে এরোপ্লেন থাকে শুন্যটা তাহলে সবাই কয়টা করে এরোপ্লেন পাবে? তারমানে আমার কাছে কোনো প্লেনই নেই তো দিব কি? সবাই শুন্যটা করেই পাবে (অর্থাৎ এখানে ভাজ্য বা যাকে ভাগ করা হবে সে শুন্য) \frac ০ ৩ = ০ টা করে (আমার কাছে আছেই তো শুন্যটা এরোপ্লেন তাহলে সবাইকে শুন্য টার থেকে কম বা বেশি করে দেওয়া সম্ভব না)

৩। q এর মান শূন্য হলে তো ফলাফল সবসময়ই অসংগায়িত হবে কারন শুন্য দিয়ে তো কোন কিছুকে ভাগ করা যায়না!
এই ঘটনাটাও হালকা ভাবে ব্যাক্ষা করা হল:
এখানে মনে করি আমার কাছে এরোপ্লেন আছে ৬টা এগুলো আমার শুন্য জন প্রানের বন্ধুকে ভাগ করে দিব (অর্থাৎ এখানে ভাজক বা যে ভাগ করবে সে শুন্য) এখানে আমার কোনো বন্ধুই নাই তো এরোপ্লেন গুলো কাকে দিব, অনততঃ একজন থাকলেও তো তাকে সবগুলো প্লেন দিয়ে দিতাম কিন্তু এখানে দেওয়ার মত কেউ নেই জন্য ভাগ ব্যাপারটাই ঘটতেছেনা! তাই \frac ৬ ০ = অসংজ্ঞায়িত; যখন এরকম ভাগ করা যায়না ( ভাজকই তো নেই তাইলে ভাগটা করবে কে) ব্যাপারটাকে তখন গনিতের ভাষায় অসংজ্ঞায়িত বলা হয় অর্থাৎ সংজ্ঞায়িত করা যাচ্ছেনা।

৪। কেউ কেউ বলতে চায় p ও q কে পরস্পরের সহমৌলিক হতে হবে অর্থাৎ p ও q এর কোন কমন উৎপাদক বা ভাজক থাকা যাবেনা। যেমন, \frac ৪ ৮ হওয়া যাবেনা \frac ১ ২ হতে হবে (যদিও \frac ৪ ৮ আর \frac ১ ২ সমান), একইভাবে \frac {৬} {১৫} হওয়া যাবেনা \frac ২ ৫ হতে হবে!

মূলদ সংখ্যা আবার ২ প্রকার:
১। পূর্ণসংখ্যা বা integer (ℤ)
২। ভগ্নাংশ বা fraction

১। পূর্ণসংখ্যা বা integer (ℤ): পূর্ণসংখ্যা তো নাম দেখেই বোঝা যাচ্ছে কেমন ধরনের সংখ্যা এরা। integer অর্থই হল পূর্ণসংখ্যা। integer এসেছে ল্যাটিন শব্দ integer থেকে যার অর্থ whole বা সমস্ত। সকল পূর্ণসংখ্যার সেট হল ℤ আর ℤ এসেছে জার্মান শব্দ Zahlen থেকে যার অর্থ number বা সংখ্যা। তো এই মহামান্য ℤ এর মধ্যে আছে শুন্য সহ সকল ধনাত্নক ও ঋণাত্নক পূর্ণ সংখ্যা।

পূর্ণসংখ্যা বা integer হল তিন (মতান্তরে ২) প্রকার:
a. ধনাত্নক পূর্ণ সংখ্যা
b. ঋনাত্নক পূর্ণ সংখ্যা
c. শুন্য বা ‘০’ (যাঁরা পূর্ণসংখ্যাকে ২ ভাগে ভাগ করেন তাঁরা শুন্যকে ধনাত্নক পূর্ণ সংখ্যার সাথে জুড়ে দেন)

ধনাত্নক সংখ্যা তো আমরা সবাই চিনি, positive numbers, শুন্যের থেকে বড় সকল সংখ্যাই ধনাত্নক সংখ্যা আর শুন্যের থেকে বড় সকল ধনাত্নক পূর্ণ সংখ্যাই হল ধনাত্নক পূর্ণ সংখ্যা বা positive integer। আবার শুন্যের থেকে ছোট সকল সংখ্যাই ঋনাত্নক সংখ্যা আর শুন্যের থেকে ছোট সকল ঋনাত্নক পূর্ণ সংখ্যাই হল ঋনাত্নক পূর্ণ সংখ্যা বা negative integer।

আর শুন্যের কথা কি বলব! একেতো এর নিজের কোনো অর্থ নেই তার উপর গুন ভাগের সময় নানা রকম আকাম করে বেড়ায় অথচ ইনি ছাড়া ১০ ভিত্তিক সংখ্যা গননায় বড় বড় হিসাব নিকাশ অসম্ভব প্রায়। যেমন, কি সহজে ৩\times১০^৮ লিখে ফেললাম আবার ৩০০০০০০০০ লিখতে গেলেও ইনার গুরুত্ব কতখানি তা সহজেই বোঝা যাচ্ছে।

আর ধনাত্নক ঋনাত্নক বলতে কি বোঝায় তা তো আমরা সবাই খুব ভালোমতই জানি যে কোনো জিনিসের বাড়তি বা উপস্থিতি হল ধনাত্নক যেমন, আমার কাছে ৫ টাকা আছে বা আমার বন্ধুর কাছে ১০টা মুরগী আছে কিন্তু ঋনাত্নক বলতে কোনোকিছুর ঋণ বা ঘাটতি বোঝায় যেমন, আমার কাছে মাইনাস ৫ টাকা আছে তার মানে হল আমার কাছে কোন টাকা তো নেই ই উল্টা ৫ টাকা ধার বা ঋণ হয়ে আছে অর্থাৎ কেউ আমার কাছে ৫ টাকা পায়। আর শুন্য হল আমার কাছে কোনো টাকাও নেই আবার আমার কোনো ঋণও নেই এরকম ব্যাপার।
positive integer বা ধনাত্নক পূর্ণ সংখ্যার ব্যাপারে আরেকটা কথা হচ্ছে যে ইংরেজিতে কেউ কেউ zero (0) সহ সকল ধনাত্নক পূর্ণ সংখ্যাকে whole number বলে তাই এদেরকে 𝕎 দিয়ে প্রকাশ করা হয় আর zero (0) বাদে সকল ধনাত্নক পূর্ণ সংখ্যাকে natural number বা counting number বলে তখন এদেরকে ℕ দিয়ে প্রকাশ করা হয়।

ধনাত্নক পূর্ণ সংখ্যা আবার ৩ প্রকার:
১। মৌলিক সংখ্যা
২। অমৌলিক বা যৌগিক সংখ্যা
৩। এক বা ১!!

এছাড়াও ধনাত্নক পূর্ণ সংখ্যাকে আরো দুই ভাগে ভাগ করা যায়:
১। জোড়
২। বিজোড়
জোড়-বিজোড় সংখ্যাও তো আমরা সবাই চিনি, যে সকল সংখ্যাকে ২ দিয়ে ভাগ করলে ভাগফল শূন্য (০) হয় অর্থাৎ যে সকল সংখ্যা ২ দিয়ে নিঃশেষে বিভাজ্য হয় তারা জোড় সংখ্যা। যেমন, ২, ৩২, ১২৩৪১০, ৭৬৫৪৩০১০৮, ১০০০০১৪ ইত্যাদি। আর যে সকল সংখ্যাকে ২ দিয়ে ভাগ করলে ভাগফল এক (১) হয় অর্থাৎ যে সকল সংখ্যা ২ দিয়ে নিঃশেষে বিভাজ্য হয় না তারা বিজোড় সংখ্যা। যেমন, ১, ৩, ১২৩৪১, ৭৬৫৪৩০১, ১০০০০১ ইত্যাদি। কোনো সংখ্যা যত বড় বা ছোটই হোক শেষের অংকটি জোড় হলে পুরো সংখ্যাটাই জোড় আর কোনো সংখ্যা যত বড় বা ছোটই হোক শেষের অংকটি বিজোড় হলে পুরো সংখ্যাটাই বিজোড় হয়।

মৌলিক সংখ্যা হল pure বা চরিত্রবান সংখ্যা। তারমানে কি গুরু? আচ্ছা তারমানে ওরা হল নিখাঁদ ওদের মধ্যে এক আর ওরা ছাড়া আর কোনো ভেজাল নেই (১০০ পার্সেন্ট খাঁটি সরিষার তেলের মত!) অর্থাৎ যে সকল সংখ্যাকে এক আর ওই সংখ্যা নিজে ছাড়া অন্য সংখ্যা দিয়ে নিঃশেষে ভাগ করা যায় না বা এক আর ওই সংখ্যা নিজে ছাড়া আর অন্য কোনো ভাজক নেই তাদেরকে মৌলিক সংখ্যা বলে। যেমন, ৫, ১৯, ৯৭১ ইত্যাদি ইত্যাদি।

আর অমৌলিক বা যৌগিক সংখ্যা হল impure বা চরিত্রহীন সংখ্যা তারমানে ওদের মধ্যে ভেজাল আছে (১০০ পার্সেন্ট খাঁটি সরিষার তেলের মত না!) অর্থাৎ যে সকল সংখ্যাকে এক আর ওই সংখ্যা নিজে ছাড়া আরো অন্য সংখ্যা দিয়ে ভাগ করা যায় বা এক আর ওই সংখ্যা নিজে ছাড়া আরো এক বা একাধিক ভাজক বা উৎপাদক বা গুননীয়ক আছে তাদেরকে যৌগিক সংখ্যা বলে। যেমন, ৪, ১০০, ১০০১১ ইত্যাদি ইত্যাদি।
বলে রাখা ভাল যে, উৎপাদক, গুননীয়ক, ভাজক সব একই জিনিস ভিন্ন ভিন্ন নাম মাত্র! (ভিন্ন ভিন্ন নাম দেখিয়া কেউ বিভ্রান্ত হইবেন্না) কেউ কেউ আবার উৎপাদক আর গুননীয়ক এর মধ্যে কিঞ্চিত পার্থক্য করতে চায় যেমন, ৬ এর গুননীয়ক হল ১,২,৩,৬ আর ৬ এর উৎপাদক হল ২,৩,৬ অর্থাৎ ১ সহ সকল ভাজক হল গুননীয়ক আর ১ বাদে সকল ভাজক হল উৎপাদক। কিন্তু বাস্তবে এই কথার কোনো ভিত্তি নাই তবে এখানে আরো দুইটা কথা আছে।

একটা হল প্রকৃত উৎপাদক: কোনো সংখ্যার নিজে বাদে বাকী সকল উৎপাদক হল তার প্রকৃত উৎপাদক যেমন, ৬ এর বেলায় ১,২,৩ হল তার প্রকৃত উৎপাদক।
আরেকটা হল মৌলিক উৎপাদক: কোনো সংখ্যার উৎপাদক গুলোর মধ্যে যেগুলো মৌলিক সংখ্যা কেবলমাত্র তাদেরকে ঐ সংখ্যার মৌলিক উৎপাদক বা মৌলিক গুননীয়ক বলে যেমন, ৬ এর বেলায় ২ ও ৩ হল তার মৌলিক গুননীয়ক। আবার ১২ এর গুননীয়কগুলো হল ১,২,৩,৪,৬ ও ১২। কিন্তু এর মৌলিক গুননীয়ক হল ২ ও ৩।
আরেকটা কথা হল, যেকোনো সংখ্যাই যেকোনো সংখ্যার ভাজক হতে পারে যেমন ৫ কে ২ দিয়ে ভাগ করলে হয় ২.৫ তাহলে ২ হল ভাজক আর ৫ ভাজ্য আবার ২ কে ৫ দিয়ে ভাগ করলে হয় ০.৪ এক্ষেত্রে ৫ হল ভাজক আর ২ ভাজ্য কিন্তু এখানে উৎপাদক, গুননীয়ক, ভাজক এসব আলোচনার সময় ভাজক বলতে কোনো সংখ্যা যেসব সংখ্যা দিয়ে নিঃশেষে বিভাজ্য হয় তাদেরকে বোঝানো হয়েছে।

নিচের ছবিটি দেখি:

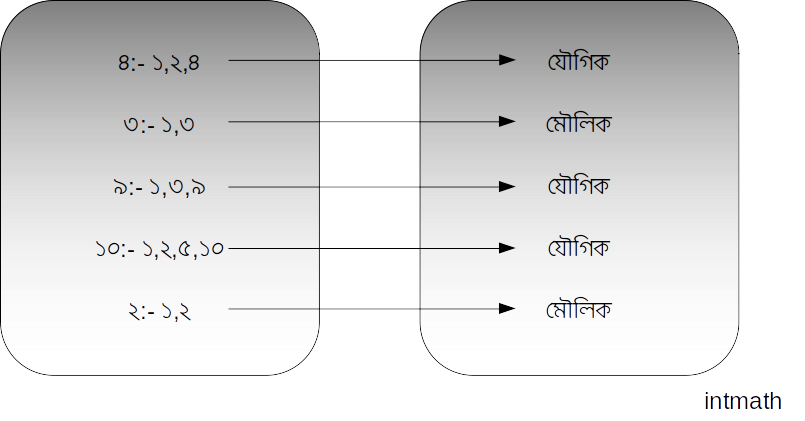
কোনো সংখ্যা মৌলিক নাকি যৌগিক তা আমরা নিচের ছোট্ট পরীক্ষার মাধ্যমেও বুঝতে পারি।

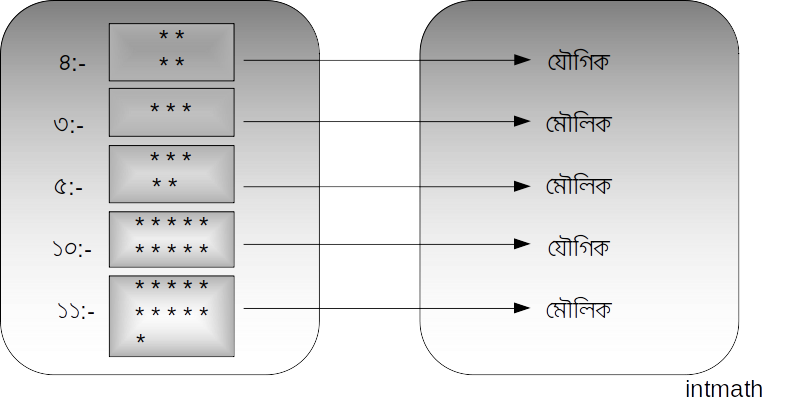
এখানে, উপরের চিত্র থেকে দেখা যাচ্ছে যৌগিক সংখ্যার ফোটা বা বিন্দু গুলোকে আয়ত আকারে সাজানো যায় কিন্তু মৌলিক সংখ্যার ফোটা বা বিন্দু গুলোকে ওরকম আয়ত আকারে সাজানো সম্ভব হয়না।

এখন ১ এর ব্যাপারটা হালকা করে দেখে নিই, ১ যৌগিক না এটা তো সবাই জানি কিন্তু মনে খটকা লাগে যে মৌলিকও না কেন, আচ্ছা মৌলিক সংখ্যার সংগা টা আরেকবার দেখে নেই ” যে সকল সংখ্যাকে এক আর ওই সংখ্যা নিজে ছাড়া অন্য সংখ্যা দিয়ে ভাগ করা যায় না তাদেরকে মৌলিক সংখ্যা বলে” তারমানে কোনো সংখ্যাকে মৌলিক হতে হলে তার সর্বনিম্ন আর সর্বোচ্চ দুইটি ভাজক থাকতে হবে। একটা হল সে নিজে আর অন্যটা হল ১। কিন্তু বেচারা ১ এর দিকে তাকালে আমরা দেখতে পাই যে তাকে ১ ছাড়া আর কোনো সংখ্যা দিয়ে নিঃশেষে ভাগ করা যায় না অর্থাৎ তাকে ১ দিয়ে নিঃশেষে ভাগ করা যায় এবং সে নিজেও ১ তাই তার একটা মাত্র ভাজক আর এই একটা মাত্র ভাজক নিয়ে সে মৌলিক সংখ্যার সংগা টাকে সন্তুষ্ট করতে পারছে না (বেচারা) সেজন্য বেচারা এক (১) মৌলিক সংখ্যা হতে পারলনা (আফসোস)। এজন্য সবচেয়ে ছোট মৌলিক সংখ্যাটা হল ২ আর আশ্চর্যের বিষয় হল ২ একটা জোড় সংখ্যা তারমানে দাঁড়াল আমাদের সবচেয়ে ক্ষুদ্রতম মৌলিক সংখ্যাটা হল একটা জোড় সংখ্যা আর সেটা হল ২!!

আচ্ছা সবকিছু তো খুব বুঝলাম কিন্তু আমার মনে আরেকটা খটকা আছে সেটা হল ঋণাত্নক সংখ্যা কি মৌলিক হতে পারে? উত্তর হল, না, পারেনা। যেমন, ৭ একটি মৌলিক সংখ্যা কিন্তু মাইনাস ৭ বা “-৭” মৌলিক সংখ্যা না। শ্রেণীবিভাগের ছক থেকেও আমরা দেখতে পাই যে, কেবল মাত্র ধনাত্নক পূর্ণ সংখ্যাদের কে মৌলিক, যৌগিক ইত্যাদি ভাগে ভাগ করা হয়েছে।

এখানে আরো কয়েকটা জিনিস হালকা করে দেখে নিই:
i. co-Prime: co-Prime এর বাংলা অর্থ হল সহমৌলিক আর সহমৌলিক অর্থ হল পরস্পরের মৌলিক, অর্থাৎ যেকোনো দুই বা ততোধিক সংখ্যার মধ্যে যদি ১ ছাড়া আর কোনো সাধারন উৎপাদক না থাকে তাহলে তারা পরস্পরের সহমৌলিক। যেমন, \frac ৮ {১৫}, \frac ৯ {১৪}, \frac {১০} {২১} ইত্যাদি।
এখানে ৮ ও ১৫, ৯ ও ১৪, ১০ ও ২১ পরস্পরের সহমৌলিক। আবার ৭, ১০, ২৭ ও পরস্পরের সহমৌলিক।

ii. pseudo-Prime: pseudo অর্থ false বা মিথ্যা, তারমানে কি pseudo-Prime অর্থ মিথ্যা-Prime বা মিথ্যা-মৌলিক? হুম, pseudo-Prime হল যেসকল সংখ্যাকে আপাত ভাবে (শুধু চোখের দেখায় মনের দেখা নয়ত) মৌলিক বলে মনে হয় কিন্তু আসলে তারা যৌগিক। যেমন, 341, 391, 1909, 13111 ইত্যাদি। এদেরকে আপাত ভাবে দেখে মনে হয় মৌলিক সংখ্যা কিন্তু আমরা একটু চেষ্টা করলেই দেখতে (মনের দেখা) পারব যে আসলে তারা (মহা ধড়িবাজ টাইপের) যৌগিক সংখ্যা। এদের সাধারনত ১ আর এরা নিজেরা বাদে খুব অল্প সংখ্যক (১ টা বা ২টা) উৎপাদক থাকে, উৎপাদক গুলো আবার সাধারনত মৌলিক উৎপাদক হয়ে থাকে।
iii. Perfect number:

এখন দেখি ভগ্নাংশ বা fraction,
২। ভগ্নাংশ বা fraction: ভগ্নাংশ হল ভগ্ন অংশ মানে কোন কিছুর ভাংগা অংশকে তার ভগ্নাংশ বলা হয়। যেমন, কারো কাছে একটা আস্ত আরেকটা অর্ধেক মানে দেড় টা রুটি থাকলে তার রুটির সংখ্যা হল ১.৫ বা \frac ৩ ২ বা ১\frac ১ ২।
এর ইংরেজি প্রতিশব্দ হল fraction আর fraction এসেছে Latin word “fractus” থেকে যার অর্থ broken বা ভাঙ্গা। আসলে দুটি সংখ্যার ভাগ, অনুপাত এবং ভগ্নাংশ একই অর্থ প্রকাশ করে। যেমন, ৩÷৪, ৩∶৪ এবং \frac ৩ ৪ সব একই জিনিস।

আমরা ভগ্নাংশদেরকে ২ রকম ভাবে লিখে থাকি:
১। সাধারন ভগ্নাংশ
২। দশমিক ভগ্নাংশ

১। সাধারন ভগ্নাংশ: যখন কোনো ভগ্নাংশকে দুইটা পূর্ণ সংখ্যার অনুপাতে (লব∶হর) বা \frac {লব} {হর} আকারে লেখা হয় তখন তাকে সাধারন ভগ্নাংশ বলে। এই ভগ্নাংশে Radix point বা দশমিক বিন্দুর ব্যবহার হয়না। এখানে লব ও হর দুইটি পূর্ণ সংখ্যা এবং লব ≠ ০। লব কেন শুন্য হতে পারেনা তা তো আগেই দেখেছি।

সাধারন ভগ্নাংশ আবার ২ প্রকার:
১। Proper বা প্রকৃত ভগ্নাংশ
২। Improper বা অপ্রকৃত ভগ্নাংশ

যেসব ভগ্নাংশের হরের থেকে লব ছোট তাদেরকে প্রকৃত ভগ্নাংশ বলে। যেমন, \frac ১ ২ , \frac ৫ ৭ ইত্যাদি আর যেসব ভগ্নাংশের হরের থেকে লব বড় তাদেরকে অপ্রকৃত ভগ্নাংশ বলে। যেমন, \frac ৩ ২ , \frac ৭ ৫ ইত্যাদি। আবার একটু খেয়াল করলেই আমরা বুঝতে পারব যে \frac ৩ ২ আর ১\frac ১ ২ একই জিনিস আবার \frac ৭ ৫ আর ১\frac ২ ৫ ও একই জিনিস। তো ১\frac ১ ২, ১\frac ২ ৫ এদেরকে আবার মিশ্র ভগ্নাংশ বলে। অর্থাৎ যে সব ভগ্নাংশের একই সাথে একটা পূর্ণ অংশ এবং একটা ভগ্ন অংশ থাকে তাদেরকে মিশ্র ভগ্নাংশ বলে। তাহলে অপ্রকৃত আর মিশ্র হল একই ভগ্নাংশের দুইটি ভিন্ন রুপ।

২। দশমিক ভগ্নাংশ: দশমিক ভগ্নাংশের ইংরেজি নাম হল Decimal fraction। যে সকল ভগ্নাংশকে প্রকাশ করার জন্য Decimal point বা দশমিক বিন্দু ব্যাবহার করা হয় তাদেরকে দশমিক ভগ্নাংশ বলে। এক্ষেত্রে ভাঙ্গা অংশকে দশমিক বিন্দুর পরে এবং পূর্ণ অংশকে দশমিক বিন্দুর আগে লিখতে হয়। যেমন, ১.৫ হল দেড় বা ১\frac ১ ২ এর দশমিক ভগ্নাংশ। আসলে ১.৫, \frac ৩ ২ আর ১\frac ১ ২ সব একই জিনিস। আবার দশমিক, শতাংশ বা পার্সেন্ট (%), ঋণাত্নক সূচক ও একই অর্থ প্রকাশ করে। যেমন, ০.০১, ১%, ১০^-২ এরা সবাই আসলে \frac ১ {১০০}।

১। সসীম দশমিক ভগ্নাংশ বা Terminating decimal fraction
২। অসীম দশমিক ভগ্নাংশ বা Recurring decimal fraction

যেসব দশমিক ভগ্নাংশের দশমিক বিন্দুর পরে সসীম (সীমা আছে যার) ঘর পর্যন্ত অংক থাকে তাদেরকে সসীম দশমিক ভগ্নাংশ বলা হয়। যেমন, ১.৭৫, ০.২৫, ১৬.৫৭৪০৩৩ ইত্যাদি। আর যেসব দশমিক ভগ্নাংশের দশমিক বিন্দুর পরে অসীম (সীমা নাই যার) ঘর পর্যন্ত অংক থাকে অর্থাৎ দশমিক বিন্দুর পরে অসীম সংখ্যক অংক বারবার আসতেই থাকে তাদেরকে অসীম দশমিক ভগ্নাংশ বলা হয়। যেমন, ১.৩৩৩৩৩৩৩….. এখানে অসীম ঘর পর্যন্ত ৩ বারবার আসতেই থাকে। আবার ২.২১৩১৩১৩…….. এখানে ১৩১৩…. এভাবে বারবার ১ আর ৩ পরপর আসতেই থাকে, আবার যদি পরপর অনেকগুলো ঘরের অংক বারবার আসতেই থাকে তাও সে অসীম দশমিক ভগ্নাংশ হবে। যেমন, ৩.১৪২৮৫৭১৪২৮৫৭১৪…….. এভাবে ১,৪,২,৮,৫,৭ বারবার আসতেই থাকে।

এখানে সুন্দর একটা ব্যাপার আছে, আর সুন্দর ব্যাপারটা হল পৌনঃপুনিক বা repeating decimal বা recurrence: ১.৩৩৩৩৩৩৩….. এখানে অসীম ঘর পর্যন্ত ৩, ২.২১৩১৩১৩…….. এখানে অসীম ঘর পর্যন্ত ১ আর ৩, ৩.১৪২৮৫৭১৪২৮৫৭১৪…….. এখানে অসীম ঘর পর্যন্ত ১,৪,২,৮,৫,৭ লেখা তো অসম্ভব অথবা দশমিকের পরে কয়টা ঘর পর্যন্ত লিখলেই বা বুঝব যে কতগুলো অংক বারবার আসবে, এসব কেমন জানি একটা মুশকিলের ব্যাপার। এই মুশকিলের সমাধান প্রকল্পে এসেছে পৌনঃপুনিক চিহ্ন বা recurrence symbol এটা এমন আহামরি কিছুই না এটা একটা ফোঁটা বা বিন্দু চিহ্ন যাকে repeating digit এর মাথার উপর বসাতে হয়। যেমন, ১.৩৩৩৩৩৩৩….. না লিখে ১.\dot ৩ লিখলেই হয়ে যায়। অর্থাৎ যার মাথার উপর পৌনঃপুনিক চিহ্ন থাকবে সে বারবার repeat করবে এটাই বোঝা যায়। তাহলে ২.২১৩১৩১৩…….. এখানে কি করব, এখানে তো repeating digit দুইটা ১ আর ৩। এখানে ২.২\dot ১ \dot ৩ হবে। ১ আর ৩ এর মাথায় পৌনঃপুনিক চিহ্ন দিয়ে বোঝানো হয় যে অসীম পর্যন্ত ১ আর ৩ বারবার আসতেই থাকে। তাহলে ৩.১৪২৮৫৭১৪২৮৫৭১৪…….. এর বেলায় কি করব? ১ থেকে ৭ পর্যন্ত সবগুলোর মাথায় একটা করে পৌনঃপুনিক চিহ্ন বসাবো? অবশ্যই না, এক্ষেত্রে শুধু ১ আর ৭ এর মাথায় একটা করে পৌনঃপুনিক চিহ্ন দিলেই বোঝা যায় যে ১ থেকে ৭ পর্যন্ত সবগুলো অংকই বারবার আসতে থাকবে। যেমন, ৩.\dot ১৪২৮৫\dot ৭।

আচ্ছা তো ভগ্নাংশদেরকে কি সংখ্যারেখার উপর জায়গা দেয়া যায়? হ্যাঁ অবশ্যই যায়। নিচের ছবিটি দেখি:

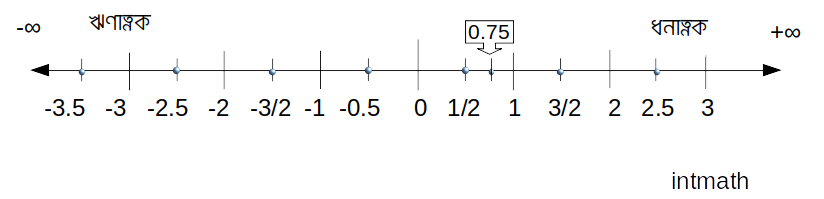
2. Irrational বা অমূলদ সংখ্যা: আমরা তো একটু আগে খুব করে অসীম দশমিক ভগ্নাংশ শিখে আসলাম। এখন কথা হল দশমিক বিন্দুর পরে অসীম সংখ্যক repeating ভ্যালুর পরিবর্তে যদি অসীম সংখ্যক non-repeating ভ্যালু আসতে থাকে তখন ব্যাপারটা কি হবে? তখন ব্যাপারটা Irrational বা অমূলদ সংখ্যা হবে। অর্থাৎ যে সকল দশমিক ভগ্নাংশে দশমিক বিন্দুর পরে অসীম সংখ্যক non-repeating ভ্যালু আসতেই থাকে তাদেরকে অমূলদ সংখ্যা বা Irrational Number বলে।

যেমন, π এর মান ৩.১৪১৫৯২৬৫৩….. এভাবে একের পর এক অংক আসতেই থাকে কিন্তু পরের অংকটি কি আসবে তা বোঝা যায় না অর্থাৎ এক্ষেত্রে একটা নির্দিষ্ট ঘর পর্যন্ত পরপর একই অংকের পুরাবৃত্তি ঘটেনা, \sqrt ২ এর মান ও তাই ১.৪১৪২১৩…… এভাবে non-repeating value আসতে থাকে তাই এরা সবাই অমূলদ সংখ্যা।
অন্য কথায় বলা যায়, যে সকল সংখ্যাকে দুইটি পূর্ণ সংখ্যার অনুপাত আকারে প্রকাশ করা যায় না তাদেরকে অমূলদ সংখ্যা বলে। যেমন, ১.৩৩৩৩৩৩৩৩ এটা মূলদ সংখ্যা কেননা একে \frac ৪ ৩ (৪ ও ৩ এর অনুপাত) আকারে লেখা যায়। কিন্তু π বা ৩.১৪১৫৯২৬৫৩….. \sqrt ২ বা ১.৪১৪২১৩….. এদেরকে এরকম লব:হর বা \frac {লব} {হর} আকারে লেখা যায় না।

** অমূলদ সংখ্যা নিয়ে পরবর্তী পোষ্টে ব্যাপক আলোচনা হবে ইনশাল্লাহ।

তো এই হল আমাদের Number বা সংখ্যা নিয়ে সংক্ষিপ্ত আলোচনা।